Mereotopology and Computational Representations of the Body

Introduction

Husserl scholar Donn Welton asks ¹ “how does one understand the relationship between a natural scientific description of the body and a phenomenological one?” In this essay I take this question in a computational context. This means asking for an understanding of the relationship between computational descriptions of the body from the natural sciences and computational descriptions from a phenomenological viewpoint. It is not clear at first that phenomenology could lead to computation at all. However, I aim to show that this is a possibility by using computational ways of thinking that have developed from mereotopology, a philosophical account of space developed by Alfred North Whitehead ².

Tensions between the space of scientific things and the space of the lived-body have been theorised by several generations of phenomenological writing, including Husserl, Heidegger, Merleau-Ponty ³, but it is the possibility of computation within these tensions that is at issue here. The natural scientific body is frequently subject to computational representation, and this is an aspect of its scientific description, but how might computation help in understanding the lived-body as opposed to the objective one?

The body, however conceived or experienced, moves or at least observes motion in space. Mereotopology arose in the context of a number of scholars, including Poincaré ⁴ and de Laguna ⁵ who were aware of a mismatch between the prevailing mathematical theories of space and the bodily experience of space. One issue here was that mathematical space started with the concept of a point, something in its idealization as an infinitesimally small entity that is outside human experience. Whitehead advanced a theory of space in which the primary components were not points but ‘regions’. Here, the term region should be understood as simply a portion of space that might, depending on the context, be two-dimensional or three-dimensional. This predated digital computation, and was not developed as a mathematical theory by Whitehead.

Today’s representations of space that typically underlie computational descriptions of the body are overwhelmingly based on co-ordinate geometry. This is especially true of systems that capture the motion of individual bodies in detail down to the level of movement of particular joints as well as of systems that represent the movement of bodies in space on a larger scale such as within a city during the course of a day. These computational representations are well suited to Welton’s “natural scientific description of the body” but are not the only computational representations available. One of the alternatives, that is well established within Artificial Intelligence (AI), originates directly from Whitehead’s mereotopology. This alternative is known in computer science as the qualitative approach to the representation of space ⁶. It is qualitative in the sense I will explain in the next paragraph. The qualitative approach is often referred to as Qualitative Spatial Representation (QSR), although the significance of logic within this framework is sometimes highlighted in the terminology Qualitative Spatial Reasoning. The intimate connection between space and time means that some authors add ‘temporal’ as well to the name. In this essay I will use QSR to refer to include all of these aspects of the qualitative approach.

One of the motivations for QSR is the need for what in the AI setting is known as ‘commonsense’ spatial knowledge. When describing bodily configurations and movements we use qualitative terminology: ‘outstretched arms’, ‘hunched up’, ‘ambling along’, instead of specifying that the arms are at some numerical angle to the line of the spine or that the distances between finger tips and shoulders exceed some quantitative threshold. Giving the location of one body part relative to another is done in terms of qualitative spatial relationships such as ‘touching’, ‘close to’, ‘crossing’, ‘enclosing’ and so on. These are ‘commonsense’ terms in that they form part of everyday spatial discourse and do not depend on specialized knowledge of geometry. QSR provides a way of representing aspects of the spatial knowledge expressed in terms of this kind in a computational way.

I will explore in more detail below the content of QSR. At this point, the idea of representing qualitative spatial knowledge computationally already suggests a question: could QSR have a role in computing with subjective corporeal experience? As Iris Young argues ⁷ in the specific context of the female, the lived-body leaves traces of subjective experience through the way it moves in the world. Could QSR be used to compute qualitative types of movement and from these understand ways of being-in-the- world?

This essay has started with two observations: the first that mereotopology arose from a mismatch between the space of bodily experience and the available mathematical representations of space, and the second that mereotopology has a computational realization. These two observations raise the central question of the article: the question of whether the computational formulation of mereotopology might provide a computational realization of bodily experience, a way of computing with the phenomenological aspect of the body as opposed to the natural scientific one. I proceed by examining next the nature of mereotopology and of its computational realization, QSR. This leads to a consideration of the use of mereotopology in the work of Stamatia Portanova and the question of how computational mereotopology might relate to this work. However, it appears that computation of bodily experience is more likely to arise not directly from the pure application of mereotopology but from the combination of the qualitative and the quantitative. In particular, qualitative relations can be used computationally as abstractions from quantitative data instead of being seen as an alternative and separate representation. This leads in the conclusion of the essay to a potential computational realization of Young’s proposal that the lived-body leaves traces of subjective experience through the way it moves in the world.

Mereotopology as opposed to co-ordinate Geometry

To understand the relationship of computational mereotopology, or QSR, to bodily computation it is necessary to consider what mereotopology is and how its origins lie in a philosophical critique of the mismatch between the spatial world as conventionally represented mathematically and the spatial world as corporeal experience. I start with geometry, its computational representation, and the distinction between geometry and topology. This enables the introduction of mereotopology and the understanding that some of its content is opposed to key aspects of the theory of topological spaces. Thus mereotopology is seen to be at variance with the conventional approach to topology.

Euclidean geometry has a familiar computational representation in co-ordinate geometry. What is less well-known is that mereotopology, despite having no quantitative content, can also be represented computationally. We examine this representation in the form of the Region-Connection Calculus (RCC). The RCC is just one part of the field of QSR.

Euclidean Geometry is rigid. Two triangles in the plane where one can be transformed into the other by rigid motions that do not change lengths or angles are essentially the same triangle, that is Euclidean geometry cannot distinguish them. Topology is more flexible. A triangle and a circle are topologically indistinguishable because the bending of the triangle’s sides to become the circumference of the circle is a continuous transformation, more precisely an invertible, or reversible, continuous transformation that does not change the topological properties of the triangle. The distinction between Euclidean geometry and topology is exploited by De Landa ⁸ in expounding Deleuze’s use of difference. Euclidean geometry has more differences than topology, as in the example of the circle and the triangle. However, we shall see that topology, in the mathematically conventional sense of ‘point-set topology’ still makes distinctions that appear to have no part in bodily experience.

Euclidean geometry is not inherently quantitative. To measure a distance between two points and arrive a number is not part of the geometry itself. Purely geometric notions only allow the comparison of one length with another, not the assignment of quantitative values. The introduction of co-ordinate geometry by Descartes opened up the way to computational representations of Euclidean geometry. This co-ordinatisation allows for efficient calculation and underlies most of the models of space used when dealing with geographical space and with bodily movement in motion capture systems to give just two examples. One of the features of co-ordinate geometry is that everything is reduced to points. The volume of a body is a collection of points, the surface of a body is a collection of points, a line such as the trajectory of a hand moving through the air is again a collection of points. The tension between points being the key components of a co-ordinate geometry model of space and points being quite outside direct human experience is just one facet of a mismatch between space as experienced and space in common mathematical models.

This mismatch is not between experienced space and computational representations but between experienced space and the underlying mathematical models themselves. Indeed, the mismatch surfaces well before the advent of digital computation. It did not originate with the philosophical and mathematical work of Alfred North Whitehead but his contribution is central to the current investigation. Whitehead’s work later became known as mereotopology, from its combination of mereology (the study of parts in relation to wholes) with topological aspects of the description of space. However, there are significant differences between mereotopology and the theory of topological spaces, so much so that the conception of mereotopology as a species of topology is potentially misleading.

The enterprise of constructing space from points has long been questioned. The questioning arises directly from considerations of bodily experience. We do not experience points; they are mathematical idealizations. Nicod ⁹, after introducing classical geometry, invites the reader to speculate: “Might the point not be the indispensable element of geometry?” He shows that, indeed, points are not essential, and that we “can conceive systems which posit the point as complex, and which are composed of terms that are easier to interpret in nature.” Being easier to interpret in nature can be understood as being related to bodily experience.

Philosophically, mereotopology provides an account of space in which regions rather than points are the primary elements of the theory. The term ‘region’ simply means a portion of space or of space-time. The key aspect of regions is that they arise from bodily experience; we can imagine moving through a three-dimensional region, a surface of finite extent can be correlated with the experience of moving the hand over a physical surface. Such regions exist as surfaces or volumes of experience without being constructed out of infinitesimal points as in a topological space. Whitehead used a binary relation of ‘extensive connection’ between regions. Following contemporary usage, ‘connection’ will be simpler and need not be distinguished from ‘extensive connection’. That connection is a binary relation means that given any two regions it is the case that they are connected or that they are not connected. Conceptually, it is simplest to imagine two-dimensional regions, and in this case two regions being connected would entail that either they overlap or that they share some portion of their respective boundaries. In a geographical example, neighbouring federal states or counties would be connected without overlapping while a constituent county would overlap the country as a whole. In the case of a physical body, regions have no such neat demarcations, but it could be argued that the thumb is connected, as a three-dimensional spatial region, to its corresponding palm without overlapping it, and the palm overlaps the hand as a whole. In another three-dimensional example, two objects in contact, such as a glass resting on a table, would be connected.

Whitehead ¹⁰ credits de Laguna ¹¹ with the basic idea of taking connection as the fundamental primitive relation between regions and also with showing how parthood could be defined in terms of connection. Saying that one region is a part of a second is just shorthand for saying that every region whatsoever connected to the first region is also connected to the second. This is, as Simons has it, not the “theoretically most satisfactory way to proceed” ¹². It combines pure mereology, the theory of parts and wholes pioneered in its rigorous development by Lesniewski ¹³, with the conceptually subsequent topological notion of connection. Mereotopology is a topological account of space in the sense that if all we know about a region is the totality of other regions with which it is connected then we cannot tell what particular geometric shape a region has. However, there is a danger in thinking that the topological rather than geometric content provides the key to a model of space that is more suitable for computing with the body.

Topological spaces are themselves based on points and the distinction between open and closed sets in a topological space does not reflect any aspect of the physical world that is open to bodily experience. This distinction depends on ‘open’ and ‘closed’ having very specific technical meanings within topology in a way that can conflict with everyday terminology. The issue has already been discussed by Randell, Cui and Cohn ¹⁴ but, in order to emphasize the distinction between topology and mereotopology, I will expand on what is involved here

I am seated at a desk. I rest my hand on the desk, experiencing a slightly cool sensation until the wooden desktop acquires heat from my hand. Qualitatively my hand is clearly on the desktop. There is no space between the two to interpose even the thinnest possible sheet of paper. This appears unproblematic, but how can this be modelled out of points? More precisely, given all the infinitely many coordinate locations in three-dimensional space, which ones belong to the desk and which to my hand? The problem comes at the boundary. We might agree that the upper surface of the desktop is 72cm above the floor. Take a point with height coordinate exactly representing this 72 centimetres, and with its other two coordinates placing it within the region of contact between my hand and the desk. Does such a point belong to the desk, or to my hand, or to both, or to neither? Distinguishing these options is essentially what is at stake in modelling each of the desk and my hand as an open or a closed set.

Without being mathematically precise, and just thinking of space as three-dimensional Euclidean space, the key idea is that a closed set includes its boundary points while an open set excludes them. The choice between modelling the desk as an open or a closed set only involves the coordinate locations exactly 72cm above the floor. If we choose the open option then these do not belong to the desk; if the closed option, then they do. This choice has no physical meaning in bodily experience – an infinitesimally thin layer of points has no physical thickness to experience unlike a sheet of paper or even the thinnest possible sheet of gold leaf. In topology, however, the difference between including and excluding this physically intangible layer is important in the mathematical theory.

There is more at stake here than the topological boundary having no thickness. The sensation of contact between my hand and the desk suggests we should not find points which are between my hand and the desk yet belong to neither. As physical experience it is clear that if my hand touches the desk then there is no intervening space. If both hand and desk include the points on their boundaries, that is are closed sets, then this denial of intervening space forces the surfaces to share points. This suggests that the desk and my hand are actually fused together, whereas we know experientially that they can be moved apart without any rupture to their physical boundaries. Alternatively, if they are open sets, then their boundary points belong to neither. Further options exist, such as one hand being modelled as an open set and the other closed, or both being neither open nor closed.

These considerations do not demonstrate that modelling the body as subsets of the conventional topological model of everyday three-dimensional space is impossible. What they do show is that such a topological model will be problematic in encouraging distinctions that do not exist in the body itself. The topological model provides an elaborate and sophisticated language allowing us to talk about points and to distinguish open and closed sets and to have sets that are neither open nor closed. To use this language, via some computational representation, to calculate with the body means a considerable overhead in translating back from the topological language to the body as experienced. The possibility of having a computational model that does not encourage a plethora of phenomenologically meaningless distinctions has been a significant motivation in developing ways of representing the commonsense world in which such distinctions are not available. One of these ways is the computational representation not of (point-set) topology but of mereotopology. Thus we move next to the examination of the Region-Connection Calculus as a computational representation of mereotopology.

Computational Mereotopology: the Region-Connection Calculus

While Whitehead was notable as a mathematician, his work on extensive connection, which led to mereotopology, was never developed by him as a detailed mathematical theory. Certain properties of connection were noted but there was no attempt by Whitehead to provide a set of axioms, such as we have for topological spaces for example. In fact, as Simons points out ¹⁵, Whitehead’s account “is not only not formally presented, but actually inconsistent”, a defect identified by Clarke ¹⁶ who also proposed an encoding of the account in a formal mathematical logic. The details of Clarke’s work ¹⁷, and subsequent logical developments of formulation are not important here; what is important is that Randell and Cohn and later Randell et al., developed a formulation ¹⁸ that was not only rendered in a formal logic, but was also in a form suited for computational representation. The Region-Connection Calculus (RCC), as this formulation became known, is a logical system which posits the existence of entities, called regions, which have between them a relation called connection. Many practically useful qualitative spatial notions including ‘overlaps’, ‘touches only at the boundary’, and ‘is equal to’ can be expressed logically just in terms of the relation of connection.

One feature of the RCC that is common to other forms of qualitative spatial and temporal representation is that it leads to a categorisation of ways that the entities it deals with can relate to each other. In the case of the RCC a number of different categorisations are possible. The simplest is just whether two regions are connected or not. A more useful set is the eightfold categorisation known as RCC-8. These are illustrated in Figure 1.

 

 

Figure 1: Eight possible relations between regions in RCC, one shaded vertically and one horizontally.

What does it mean to have a computational representation of spatial relationships such as these? If there are no lengths or distances, no shapes or angles associated with regions, no numerical values, of what does computation consist? The data in such a computation are statements, for example that two specific objects have a certain spatial relationship to each other, or that one object is not spatially connected to any other objects. One aspect of computation is then the derivation of further statements from these. In a very simple and purely mereological example, from B being a part of A and from C being a part of B, we can derive the statement that C is a part of A. More generally if we know which one of the RCC-8 relations holds between B and A and which one between C and B then we can compute what the possibilities are for the relationship between C and A.

Mereotopology as a lense

Mereotopology was partly motivated by the discrepancy between bodily spatial experience and point-based mathematical representations of space. We have seen that mereotopology has produced a computational counterpart in the Region-Connection Calculus. While logic allows computation in the RCC, it is by no means clear that basing a theory of space on regions automatically means that it will support human spatial thinking more effectively than Cartesian co-ordinate geometry. Indeed the value of computational mereotopology in this respect has been called into question. From a psychological perspective, the cognitive plausibility of certain aspects of qualitative spatial relations has been examined ¹⁹, and the question of whether the spatial ontologies arising from region-based accounts of space are actually simpler than the conventional mathematical approaches was considered by Pratt and Lemon ²⁰.

Having introduced computational mereotopology and traced its origin in spaces of bodily experience, it remains unclear how it might actually be used in a concrete scenario of bodily computation. To examine one possibility we turn to a use of mereotopology where it functions as a conceptual lens to view and relate ways of thinking about movements of the body in dance. Topology itself as a form of spatial discourse also appears widely elsewhere in the social sciences, in cultural studies, and in human geography as Martin and Secor ²¹ show in their consideration of “post-mathematical topology”. Perhaps surprisingly mereotopology does not figure in this account, but as we have already stressed, a mereotopological model of a spatial situation is not a topological space. Mereotopology is not a kind of topology in the usual mathematical (point-set) sense.

Stamatia Portanova uses “the mereotopological lens” ²² to view the dissemination and repetition of popular dance movements such as Michael Jackson’s Thriller and Psy’s Gangnam Style. This work makes use of mereotopology as a way of thinking that relates “movement ideas” and the imitable motions that constitute dance forms. The “virtual choreographic objects” in Portanova’s theory relate to the sequences of movements that can be represented by data derived from motion capture systems. The understanding that results from this theorisation comes through the use of mereotopological terminology and concepts rather than through the use of formal logic ²³. However, we shall see that as the relationship of logic to language is more fundamental than that of logic to number, the representation of statements as logical propositions allows mereotopological description in language to have a computational representation.

To speak of “when the regions of neck turning and shoulder raising are connected … ” provides a clear conceptual identification of spatio-temporal regions, but how could these regions be identified in a specific instance of the “Thriller choreographic design” being discussed? Could a practical computational mereotopology be applied in this setting? Just concentrating on the spatial, as opposed to spatio-temporal aspects, neck and shoulder are spatial regions but where do they end? Whilst tracing a route down my neck to my shoulder can I detect when my finger leaves the neck region or enters the shoulder region? Are bodies equipped with neat demarcations, like the boundaries between joints of meat in diagrammatic renderings of cattle, pigs, etc in cookery books?

It is even less clear that an arbitrary gesture, a spatio-temporal rather than a purely spatial region, could be identified and made an object of computation. Of course systems already exist that recognise a specific range of gestures that have been learned in advance, but the extraction of meaningful movements as spatio-temporal regions from an unconstrained movement of a body is quite another matter. Of all the possible regions of space time that could be identified as regions, why should certain ones be counted as important? Mereotopology is unlikely to help make such decisions and this does not appear the best route to lead to mereotopological computation in the context of dance.

An alternative possibility lies in the way that computational mereotopology uses logical statements and not numerical values. Although it is challenging to see how a ‘neck turning’ could be extracted as a spatio-temporal region in a four-dimensional space-time and then have its connection with other regions calculated automatically without already knowing that this gesture was significant, we can conceive the processing of discourse about such regions. That is, a computational representation of the “virtual choreographic objects” identified by Portanova might consist of a list of the various spatio-temporal regions involved and a list of which of them were connected to which. Such data, could be augmented by a logical encoding of the properties of the connection relation and the properties of the purely spatial arrangement of the body, in terms of what is joined to what. Assembling such data for a number of virtual choreographic objects opens the prospect of computation over the space of these virtual objects. For example, what similarities are there within this space? What fragments of the sequences of gestures in one object appear in which other objects? Such a representation could play a role analogous to the representations of movements in the languages of Laban ²⁴ or Benesch but in a significantly more qualitative manner.

Differentiated experience revealed in movement

Computation can be a means of categorizing the world, of measuring (associating numbers to things); of distinguishing one thing from another — whether individuals are the same or not, whether something counts as large or small. Computation can also be a tool to understand the world, not in a scientific determination, but by virtue of a lens through which the body can be viewed and from where an understanding of embodied space (as well as the distinctions marked by one body in relation to another) can be conveyed. Could this theoretical characterisation work in practice? Could a mereotopological computation determine whether a body is black, female, gay, handicapped, obese? What does it mean to compute such a thing? How might the distinctive category of a specific body manifest itself through an aspect of the body open to computational representation? And could mereotopology have a role in constructing this representation?

One possible source for such a representation lies in the way that movement and outward behaviour in the world reflects individuals’ inner experiences. Iris Young reported ²⁵ a number of distinctions between feminine and masculine modes of bodily movement and further interpreted what these differences reveal about underlying structures in the society some women inhabit. Young starts from a study by Straus ²⁶ of differences between boys and girls in ways of throwing a ball. Her analysis expands from this specific task to consider other bodily movements directed to specific ends. This restriction is

“… based on the conviction, derived primarily from Merleau-Ponty, that it is the ordinary purposive orientation of the body as a whole toward things and its environment which initially defines the relation of a subject to its world. Thus focus upon ways in which the feminine body frequently or typically conducts itself in such comportment or movement may be particularly revelatory of the structures of feminine existence.” ²⁷

Thus, the identification of differing modes of movement is used to uncover structures within encompassing societies. Modes of being-in-the-world are manifested through manners of bodily movement that are apparent to others, and possibly — in different ways — apparent to the individual herself. In a subsequent re-examination of the essay, Young ²⁸ finds value in the way her framework helps construct “the modalities of women’s body comportment and spatiality as contradictory”. The analysis Young provides depends on qualitative distinctions in movement. For example, “free motion”, “open reach”, “ fluid and directed motion”, “motion concentrated in one body part” are identified as styles of bodily motion that do not appear to have precise numerical definitions. Similarly, terms including “reach, extend, lean, stretch …” describe movements that are typically recognizable but are very much qualitative.

Young shows how traces of inner experience — ways of being-in-the-world — can be read from the outward movement of particular bodies in everyday tasks. Similar kinds of inner experience would be expected to leave similar kinds of traces. This should apply in Young’s case of feminine and masculine ways of moving but also, and more speculatively, in other categories of body such as black, white, gay, straight, disabled, obese, young, old, and so on. Underlying categories interact with transient inner worlds such as happy, sad, tired, anxious, hopeful, and so on. We can imagine these interactions as complex interweavings of bodily expressions that might be read as messages by others.

Deconstructing such messages, or signals, in a quantitative way — a sophisticated kind of Fourier analysis splitting the movements into combinations of atomic constituents like neat sine waves — seems a hopelessly unrealistic idea. But perhaps mereotopology could lead to a computational representation of these signals in a qualitative way? If so what would the regions be, and how might they be extracted from the world and represented as data? This seems even more difficult to imagine in practical terms of a digital implementation than extracting the regions of gestures I considered in Portanova’s analysis in the previous section. In that case I suggested that discourse might provide the raw material that computation could manipulate. This possibility arises because discourse and analysis of choreographic movement necessarily refers explicitly to spatial configurations, even if the lens is not the mereotopological one used by Portanova ²⁹. In the case of experience as revealed by the body, however, the correlation of spatial configurations and changing gestures with inner worlds is not often explicitly formulated as discourse by the individual. Analyses, such as that by Young might be used as a source of discourse for these sub-conscious gestures but these are likely to be much less detailed than in the case of the deliberate and explicit gestures of choreography.

While Young’s terminology is clearly qualitative in examples such as “free motion” cited above, it is unclear how such a generic type of movement leads to computable mereotopological regions for the motion of an individual body. Seeking a discourse yielding terms representable via a logical representation is likewise not an obvious possibility at the level of individual bodies. The role of computational mereotopology here, however, may lie not in the direct application of region-based models of space, but instead in the use of computational representations of spatio-temporal phenomena that use the relational approach to deal with the qualitative. Computational mereotopology based on spatial regions is only one aspect of the more general qualitative approach to both space and time which we examine next.

Qualitative Representation of Space and Time

Whitehead’s mereotopology, and its computational representation in the Region-Connection Calculus, focuses on relations between regions. For example, given two regions they fall into exactly one of the eight relations described earlier. Although we need have no numerical information about the location of the regions, we can still represent the qualitative spatial relationship computationally through the ability of the computer to encode logic just as readily as quantitative data.

The use of qualitative relations as a computational representation of the world is by no means restricted to the representation of space conceived as regions alone. As a first example consider not regions of space but intervals of time. In what ways can such intervals be related qualitatively? Some possibilities are readily seen: one interval may occur wholly within another, one interval may end before another starts, one interval may end at the same time as another starts, and so on. In terms of bodily movement an event, such as raising the left hand from touching the left thigh to being above the head, can have one of these temporal relationships to the event of raising the right hand in a similar way.

A set of thirteen possible relationships between time intervals in this fashion has been determined by Allen ³⁰. This is similar to the eightfold classification in the Region-Connection Calculus in that the collection of entities, spatial regions on the one hand and temporal intervals on the other, has exactly one of the relations between every pair of the entities. It is also similar that the entities have boundaries and we may speak of connection between temporal intervals in exactly the same way as between spatial regions. That is, two intervals are connected when they either overlap, sharing a common sub-interval, or when they touch at a boundary, or in other words, meet at an endpoint. However, a key feature of the Region-Connection Calculus is the way that the relation of connection alone can be used to define other relations. Saying that one region is “a non-tangential part” of another is simply a shorthand for a logically equivalent, but to humans far less comprehensible, statement in which the only relation mentioned at all is connection. This ability to reduce everything to a simple primitive relation of connection is not found in Allen’s calculus of intervals. The fact that two intervals touch at their boundary but do not overlap does not tell us which interval is earlier than the other.

 

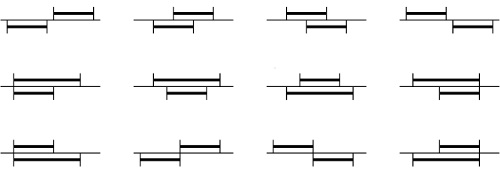
Figure 2. Twelve of the thirteen Allen Relations between temporal intervals. The thirteenth is that the intervals are equal

Allen’s intervals provide us with a qualitative language of thirteen relations. The Region-Connection Calculus leads to (but is not the same as) a qualitative language of eight relations. The significance of this from a computational point of view lies in the mechanism this provides for dealing with qualitative knowledge about the world rather than in the connections with the mereotopological view of space itself. Systems of qualitative relations are commonplace in knowledge representation. The many examples include cardinal directions, but one further case is needed here. Consider relations between trajectories in space as explored by Kurata and Egenhofer ³¹. Here the entities being related are lines in two-dimensional space – imagine traces of bodily movement, the path taken by a person across a public space for example. Just as with the thirteen Allen relations and the eight RCC relations we can consider how one trajectory relates qualitatively to another.

In Figure 3, the first diagram shows two arrows starting at the same point, crossing over once and ending in different places. The lengths of the arrows, their directions, and exactly where they cross are all irrelevant, although any specific instance will have particular values for all these things. Similarly, in the last example in Figure 3, the key qualitative feature is that the solid arrow meets first the body of the other arrow, and then the end of it and then the starting point of the other arrow before finally reaching its own end. Any two arrows having an arrangement that fits this description stand in the same qualitative relationship to each other.

 

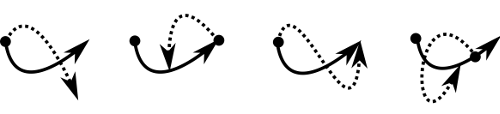
Figure 3. Example relations between arrows in the head-body-tail calculus of Kurata and Egenhofer.

The field of Qualitative Spatial Representation is thus much broader than just the computational counterpart of Whitehead’s mereotopology evidenced by the Region-Connection Calculus. It is this wider field that may well offer the most immediate route to forms of computing with the body that are capable of including representations of the phenomenological experience revealed in bodily movement as considered by Young. In the final section I examine one way in which QSR has found practical application in artificial intelligence. This involves the re-introduction of co-ordinate geometry, not in opposition to mereotopology but in collaboration with the more general QSR. This will lead finally to a concluding vision of how phenomenological experience could be introduced into a computational representation.

Co-Ordination with Geometry

QSR with a combination of space and time has been used in computing activities from video observations ³². This work aims to tell from purely visual evidence what activity is being observed. This might be unloading an aircraft or a simpler domestic scenario such as making a hot drink. In this work a sequence of frames is given which is then processed by computer vision techniques to obtain objects that are tracked through time. Objects considered in the specific setting include, for example, planes, air-bridges, and vehicles involved in activities at an airport. In an individual video frame each object is reduced to its bounding box, the smallest rectangle drawn in the space of the video frame that encloses the object. The interaction between these rectangles in each frame is assigned one of three qualitative spatial relations: the boxes overlap, they are separate, or one is inside the other (including their equality). These interactions are computed for each pair of objects in each frame and the temporal relationships between these spatial relationships are also computed.

This computational representation of objects moving in space uses two QSR calculi: the temporal interval calculus of Allen and a simplified form of the RCC-8 calculus where only three spatial relationships are possible. However, the spatial relationships are not between the actual objects themselves but between rectangles in the co-ordinate space of each video frame which are tied to the objects. The mechanism by which spatial and temporal relationships is combined is too sophisticated to review in detail here. However a bodily example should help to clarify the idea. Seen from a certain viewpoint, say in observing a particular choreography, a performer’s left hand clenched in a fist might be in front of their face and this configuration is maintained while in a shorter interval the right hand is raised above the head. Imagining the bounding boxes in a video we would see the box corresponding to the face contains within it the box corresponding to the fist and this relationship would persist for a number of frames. For a sequence of frames within the ones showing the fist in front of the face, we can also see that the boxes corresponding to the head and the right hand remain separate. The computational representation describes for each pair of objects in a spatial relationship the temporal relationship between the intervals in which the spatial relationship between those two objects was maintained.

Whitehead’s mereotopology arose from a mismatch between experience and point-based spatial thinking. Philosophically in opposition to point-based geometry, and in particular to the computational representation of co-ordinate geometry, the practical application of computational mereotopology has been found not as an alternative to this geometry but as a component of a lens through which the geometry is viewed. This is the lens of abstraction, of taking a less-detailed view; it replaces the quantitative data of where exactly in the frame-space each bounding box is located with the qualitative description of how each pair of bounding boxes is spatially related. At the temporal level, the lens replaces quantitative information about the precise frames for which spatial relationships are maintained which qualitative statements about relationships between the intervals in which this happens. In this setting the practical role of QSR does not lie in an independent way of computing with space and time. Instead QSR provides a way of abstracting from the geometric information; a way of avoiding the problem of not being able to see the wood for the trees.

Having seen how QSR can be co-ordinated with geometry, we return to the question of the possibility of a computational representation of some aspects of phenomenological bodily experience.

Relational computation and the body

In the extraction of knowledge about activities from purely visual evidence just described, two particular sequences of events in the world are recognised as instances of the same abstract activity when the lens provided by QSR for viewing the detailed geometric representation detects no difference in the two sequences. Although the application of these techniques has been, so far, in the practical domain of knowledge extraction from video in artificial intelligence, it is possible to envisage how they might play a role in a type of computational representation of phenomenological experience. Consider the description of Steinbock:

“Moving down the street, I exhibit a style of walking, a gait that is recognizable to others as “my style,” “my gait.” Each step recuperates the sedimented past; my intention towards the future … . I carve out a world through this habitual body … .” ³³

This recognizable gait expresses the author’s way of being in the world and is an example of the way that bodily movement reveals intentions, past experiences, and understandings as in the analysis Young makes of what she calls “feminine experience”. But can we use QSR to represent this phenomenological experience in a computational way? We have already seen that discerning regions, whether as spatio-temporal gestures or as purely spatial parts of the body, from visual evidence appears to be extremely challenging. The problem lying in the difficulty of deciding how to demarcate these regions and also in deciding what regions should be significant. If however we think not in terms of region-based space, but look for the application of qualitative representations from the wider field of QSR there seems to be a way forward.

The lens of QSR is used by Sridhar et al. ³⁴ to cluster changing spatial arrangements of objects which differ geometrically but which correspond to the same activity taking place. The same approach seems feasible with movements of the body in the specific case of walking. That is, QSR could be used to abstract from the kind of geometric data obtained from motion-capture systems for example. As the body walks locations on it trace out trajectories, lines in three-dimensional space of where the location has moved. Using these lines, the one-dimensional traces of movement instead of extensive regions of space or space/time avoids the difficulties highlighted earlier with these regions. The general approach is still within QSR although it is arguably not a computable form of mereotopology in Whitehead’s sense.

Consider trajectories over a fixed interval of time from just two locations of the body, say the two wrists to be specific. Recall that in the case of activity analysis from video data the spatial relationship between pairs of objects is not considered in three-dimensional space but in the space of each frame in the video. This restricted view is a projection into two-dimensional space which itself introduces some of the relationships. That is, two objects which move so as always to be separate in three-dimensional space can, when seen from the camera’s viewpoint, move so that their outlines touch and then overlap and then become so that one outline lies wholly within the other. In the work on activity analysis, the representation only uses this two-dimensional flattening but clearly events such as objects touching in three-dimensional space will result in their two-dimensional outlines touching from any point of view.

In the case of the two wrists as the body walks, observing the two trajectories from a fixed viewpoint will typically reveal a complex pattern of interaction between the trajectories. Taking a fixed interval of time and looking at our two trajectories we can consider their qualitative relationship from the chosen viewpoint. Maybe the two lines we see are separate, maybe they cross just once, maybe one contains a loop which intersects the other twice. There are different possibilities for what the qualitative lens allows to be seen from the geometric data. Maybe we only consider whether one line crosses the other or not, or maybe we take the lines together with their direction, giving us arrows as in the qualitative calculus of Kurata and Egenhofer mentioned earlier.

QSR is not a fixed body of techniques that have to be applied unchanged to new situations. Systems of qualitative relations can evolve to meet the needs of new questions such as what features of two-dimensional traces of bodily movement are characteristic of particular categories of body or, more simply, of styles of walking. These systems cannot be constructed without extensive practical experiments but what these considerations indicate is that such experiments would be worth making. Having started with mereotopology as a philosophical alternative to point-based geometry, we have reached a view in which the computational relevance of mereotopology is found by expanding from a purely regional view of space to other types of qualitative relations and by using the qualitative as an abstraction from geometric data instead of as an alternative to it. By using QSR in this way there might be a computational representation of the body in which quantitative data about precise movements is abstracted to a representation capable of revealing something of inner experience through commonalities of ways of moving. This possibility, that being in the world might be evidenced computationally through qualitative ways of moving, brings us back to Young’s proposal that the lived-body leaves traces of subjective experience through the way it moves in the world. Implementing this proposal could lead to a novel lens through which to explore the interaction between phenomenological experience and objective bodily movement.

 

References

Allen, J. F. “Maintaining knowledge about temporal intervals.” Communications of the ACM 26 (1983): 832—843.

Clarke, B. L. “A calculus of individuals based on ‘connection’.” Notre Dame Journal of Formal Logic 22 (1981): 204—218.

Clarke, B. L. “Individuals and points.” Notre Dame Journal of Formal Logic 26 (1985): 61-75.

Cohn, A. G. and Renz, J. “Qualitative Spatial Representation and Reasoning.” Eds. F. van Harmelen, V. Lifschitz and B. Porter. Handbook of Knowledge Representation. Amsterdam: Elsevier, 2008. pp551-596.

de Laguna, T. “Point, line and surface as sets of solids.” The Journal of Philosophy 19 (1922): 449-461.

DeLanda, M. Intensive Science and Virtual Philosophy London: Continuum, 2002.

Klippel, A., Li, R., Yang, J., Hardisty, F., and Xu, S. “The Egenhofer-Cohn Hypothesis or, Topological Relativity?” Cognitive and linguistic aspects of geographic space. Eds. M. Raubal et al. Berlin: Springer, 2013. pp. 195-215.

Kurata, Y. and Egenhofer, M. J. “The head-body-tail intersection for spatial relations between directed line segments.” GIScience 2006: Proceedings. Lecture Notes in Computer Science: 4197. Eds. M. Raubal et al. Berlin: Springer, 2006. pp. 269-286.

Luschei, E. C. The logical systems of Lesniewski Amsterdam: North-Holland, 1962.

Martin, L. and Secor, A. J. “Towards a post-mathematical topology.” Progress in Human Geography 38.3 (2014): 420—438.

Merleau-Ponty, M. “Selected readings.” The body. Classic and contemporary readings Ed. D. Welton. Oxford: Blackwell, 1999. pp. 150-177.

Nicod, J. Foundations of geometry and induction. London: Kegan Paul, Trench, Trubner and Co. Ltd, 1930.

Nowak, G. “The concepts of space and continuum in Poincaré’s Analysis Situs.” Henri Poincaré. Science et philosophie. Congrès international. Nancy, France 1994. Eds. J.-L. Greffe, G. Heinzmann and K. Lorenz. Berlin: Akademie Verlag, 1996. pp. 365-387.

Portanova, S. “The Mereotopological Space/Time of Dance.” Space and Culture 16.2 (2013): 194-210.

Portanova, S. “Virtual choreographic objects.” Digital movement. Essays in motion technology and performance. Eds. N. Salazar Sutil and S. Popat. Basingstoke, Hampshire: Palgrave Macmillan, 2015. pp. 67- 81.

Pratt, I., and Lemon, O. “Ontologies for plane, polygonal mereotopology.” Notre Dame Journal of Formal Logic 38(1998): 225-245.

Randell, D. A. and Cohn, A. G. “Modelling topological and metrical properties in physical processes.” Eds. R. J. Brachman, H. J. Levesque, and R. Reiter. Proceedings of first international conference on principles of knowledge representation and reasoning. San Mateo, California: Morgan Kaufmann, 1989. pp. 357-368.

Randell, D. A., Cui, Z., and Cohn, A. G. “A spatial logic based on regions and connection.” Eds. B. Nebel, C. Rich, and W. Swartout. Principles of knowledge representation and reasoning. Proceedings of the third international conference (KR92). San Mateo, California: Morgan Kaufmann, 1992. pp. 165-176.

Salazar Sutil, N. “Rudolf Laban and Topological Movement: A Videographic Analysis” Space and Culture 16.2 (2013): 173-193.

Simons, P. Parts. A study in ontology. Oxford: Clarendon Press, 1987.

Smith, B. “Mereotopology — A theory of parts and boundaries.” Data and Knowledge Engineering 20 (1996): 287—303.

Sridhar, M., Cohn, A. G., and Hogg, D. C. “Unsupervised learning of event classes from video.” Eds. M. Fox and D. Poole. Proceedings of the twenty- fourth AAAI conference on artificial intelligence. Menlo Park, California: AAAI Press, 2010. pp 1631-1638.

Straus, E. W. “The upright posture.” E. W. Strauss. Phenomenological Psychology: The Selected Papers of Erwin Straus. New York: Basic Books, 1966, pp. 137-165.

Steinbock, A. J. “Saturated intentionality.” Ed. D. Welton The body. Classic and contemporary readings. Oxford: Blackwell, 1999. pp. 178-199.

Welton, D. “Soft, smooth hands: Husserl’s phenomenology of the lived-body.” Ed. D. Welton The body. Classic and contemporary readings. Oxford: Blackwell, 1999. pp. 38-56.

Whitehead, A. N. Process and reality: An essay in cosmology. Cambridge: Cambridge University Press, 1929.

Young, I. M. “Throwing like a girl: A phenomenology of feminine body comportment motility and spatiality.” Human Studies 3 (1980): 137-156.

Young, I. M. “ “Throwing Like a Girl”: Twenty Years Later.” Ed. D. Welton The body. Classic and contemporary readings. Oxford: Blackwell, 1999. pp. 286-290.

 

Notes