Modelling biology – working through (in-)stabilities and frictions

Introduction
Computation is giving rise to new scientific practices and, specifically, new capacities for investigating the complexities of the physical and natural world. The grand claims sometimes conflate computation and science, and go so far as to imagine a ‘computational science’ replacing science as we know it (cf. Carlson, 2011). Looking past the heady rhetoric, though, questions are raised about what role computation is coming to have in science. As science studies has so compellingly illustrated, the developments in the sciences embroider a tapestry of practices and epistemes that defies simple relations between subject and object, tools and doings/knowings, etc. How then should we make sense of the relationship between computation and scientific practice? In what ways is computation taking on an agential role in what scientists do and what is at stake in the emerging entanglements of code, algorithms, software, scientists, scientific phenomena/knowledge, etc.
In this article, we reflect on questions such as these by working through the elisions and frictions performed in the development and early use of a computational tool built to model biological systems. The tool, a web-based program called the Bio-model Analyzer (BMA)¹, applies a sophisticated algorithm to rapidly determine cell fate in highly complex gene regulatory networks and specifically to test for what is referred to as ‘stability’. Naturally, the work on and around a tool that brings computation and biology together in such a way raises a host of concerns relevant for the areas of science and software studies. Our hope, here, is to draw particular attention to what arises when computation is used to represent and intervene in biology. We aim to show a concern for the entangled relations between representations and interventions in computational modelling, and the troubles that arise in a still nascent area of biology that shows, thus far, no sign of disciplinary and epistemic uniformity (Fujimura, 2011). The wider relevance of this work speaks to the relationships software models have with ways of knowing. Through our example, we illustrate how, exactly, knowledge is materialised through on-going and fluid transitions between abstractions and formalisms, and visualisations and tools. The opposing binaries of computation vs. tools, abstractions vs. phenomena, and knowing vs. doing, are contested here; foregrounded are the ways in which these worlds unceasingly entangle, surfacing frictions or multiplicities that make it resoundingly clear that computation alone is far from a stand-in for science (and how it is done). In broader terms, then, we offer a case study in how we might work through the frictions differently—how we might put computation to work in scientific life, not see it as a replacement for it.
The specific focus on biological modelling compliments other similarly motivated research in science studies and the philosophy and history of science and, in particular, the thoughtful accounts from Evelyn Fox Keller (especially her study of modelling the gene Endo16 (2002: 234-264)). We find, for instance, that biologists demonstrate a peculiar ease with incompleteness and messiness in their work, so much so that a pragmatism prevails. Omissions and inferences, as Keller (2000) remarks, are simply an expected part of building biological models. Thus, while it is undoubtedly the case that there are significant challenges in using computation to model biology—some of which hinge on the sometimes awkward analogies drawn between biology and machines (Fujimura, 2011)—our work bears out the willingness on the part of biologists to work, pragmatically, with the tensions.
Our broader results elaborate on the now established lineage in science and technology studies (STS) and feminist technoscience, one that observes how just such tensions help to productively work over what we know and how we know it (Bowker and Star, 2000; Haraway, 1991; etc.). The work we present reaffirms that as there are moments when it appears phenomena stand still and ideas are, so to speak, flattened through technology, so too are there times when the frictions enact multiple ways of knowing and enliven new possibilities. We show then that digital devices and their ubiquity do not just flatten worlds, they “proliferate circuits, they set up competing and cross-cutting scales of knowing, relating and responding, and they expose fresh margins of indeterminacy in the ensembles of people, machines, lives and things we inhabit.” (Mackenzie and McNally, 2013: 2). Thus we take as a starting point Joan Fujimura’s relevant reflections on the elisions between computing and biology:

“…these imported rules, concepts, and principles are not simply mechanical terms. They also are epistemologies that create new ontologies, that is, new realities. They can be used to manipulate systems to produce different natures, new biologies. These new biologies are and will be produced through human and material agencies.” (2011: 78).

Whilst our work adds to the continued accounts of this human-nonhuman bricolage, it aims to put into practice the theorising of difference and a “diffractive methodology”, most vigorously advanced in feminist technoscience.² As technoscience scholars such as Barad (2007), Haraway (2010) and Veran (2001) convincingly articulate, the continued studies of ontics and their relations to matter invite (if not demand) us to ask what role we have in witnessing and accounting for knowledge-making practices and their associated “regimes of existence” (Teil, 2013). Acknowledging our own active participation, they ask how we might intervene in such material enactments so that the differences and frictions are (re-)figured as productive—how they might be used for “making a difference in the world” (Barad, 2007: 90)? But, despite the thoroughness of the theorising, questions remain about what this entails in practice. As Barad (2007) contends, we have a responsibility to be responsive and act with care. What though does such responsive care look like on-the-ground, in biology? What would it look like to participate in a ‘generative working through’ with biologists?
The following, then, represents an attempt to interject our theorising back into the practical business of science and specifically computational biology. In discussing the development of BMA, our aim is to put the theorising to work, answering in some small, preliminary way Mackenzie and McNally’s wider call “to take an affirmative stance in relation to life sciences and their increasingly dynamic understandings of lives” and “to identify and explore ways of relating to those understandings in situ” (2013: 74). Our story, if you will, is one of trying to stay with the trouble in the ever-so practical business of building and using modelling tools. We want to show how in designing a software tool some different—shall we say (for now)—‘versions’ of scientific knowledge are enacted. These differences are understood as sources of friction for the tool and its design, but are too, we will show, capacities for moving on, for doing a science-in-situ that may be multiple and open to trouble.

Computational Biology in Science Studies
Computational biology is undeniably an area thick—almost impenetrably so—with numbers, mathematics, algorithms, proofs, models and unfathomably large data. Indeed, it may well be one of those subjects that instinctively triggers the impulse to “look the other way” for scholars in science and technology studies (Merz and Cetina, 1997: 73). Its work-a-day practices seem far removed from the hyped-up—glamorous even—worlds of biotech and bioengineering, worlds promising new life forms and raising attendant issues in law, ethics and proprietary invention (Birch and Tyfield 2013; Carlson, 2011; Myers, 2009; Tutton, 2011). It involves, in practice, the application of technical know-how and specialist competencies with specialised tools; activities include identifying problems and expressing them in logical terms, composing algorithms to solve these problems, and the packaging of algorithms in software tools so that they are of use and intelligible to biologists.
Unsurprisingly, though, we find computational biology, close up, does raise relevant issues for both software studies and STS. ³ Much of the work operates at the fringes of a nascent (computational) science and, by necessity, inhabits the borderlands between disciplines. In this way, it revisits many of Agar’s (2006) observations of computers first being introduced and taken up in the sciences, specifically by extending scientists’ capacities “to see” their phenomena.⁴ It also invites questions about the intermediary role of scientific models (Mattila et al., 2006) and the associated issues Edwards et al. recognise as important in their call to “investigate how data traverse personal, institutional, and disciplinary divides.” (2011: 669). As the latter make clear, despite the interest shown towards the movements and translations of data, science studies continues to silo scientific work by examining discrete and bounded disciplinary practices, therefore avoiding the “science friction” encountered when data is shared. While computational biology does not, as yet, necessitate data’s “travel far and wide” (ibid.), it does demand data be understood and used from two (and often more) disciplinary perspectives; in the merging of disciplines, biological data are, ostensibly, figured as computational resources and, in turn, the results of the computation are treated as biology. For the studies of science and computation, then, one thread of relevance would appear to be in the forms of representation, translation, collaborative practice and so on required to get the biology to make sense in computational terms and vice-versa.
It’s precisely the kinds of frictions that arise in this use of computation to represent and intervene in biology that are of interest here. Problems of translation and frictions abound with this relatively new convergence of disciplines, not least with profound questions concerning the nature of modelling and simulation in the sciences (Cartwright, 1997; 1999; Hacking, 1983; Morrison, 2009; Parker, 2009; Winsberg, 2001). But, by narrowing in on the practical business of getting computation to do biological work (and biology to do computational work), our concern is more closely aligned with how, exactly, knowledge is enacted and therefore where there might be scope for imagining a generative role for computation in the sciences. This is a perspective grounded in what is materially done (and undone) in scientific practice and how the production of scientific knowledge is never outside of the many multiples of seeing, doing, (inter-)acting, etc.
Offering an exemplary as well as relevant case for us is Myers’ (2008) account of X-ray crystallography and protein modelling. She details crystallographers’ bodily contortions describing how they enable crystallographers to competently ‘see’, ‘feel’ and consequently model proteins. Moreover, she describes the impressions these practices leave on modellers’ bodies, infusing something of the modelling tools and machines onto and into the body. Her accounts trouble the category distinctions made between model-modeller, object-subject, etc. Matter and knowing are shown to be entangled, always already united in the co-enactment of scientific work and discovery. Yet this “body-work”, as Myers refers to it, is as much about imagination as it is about fact-finding and discovery. The very “particular effective kind of handling” (Myers 2008: 38/2) afforded by computer modelling and seeing and feeling like a protein—bodily reproducing it in machine-like ways—give rise to a distinctive imagining of biology. Although our interests are less concerned with modeller’s bodies and more with the seeings and doings enacted through representations and computation, we, like Myers, want to narrow in on what the local and material work does, how it (re)imagines biology. It is, we will aim to show, through a recognition of this imagination and the making visible of the material work involved that we find room for multiplicity and generative scientific practice.
To build up this line of inquiry, we first set the backdrop to the BMA project and then explain the computational technique that underpins the tool. This may be where the technical details appear “tortuous”, to borrow MacKenzie and McNally’s apt phrase (2013: 5), but the details will be important for understanding the source of the frictions in BMA. Following this, we work through three views onto the tool and the design work surrounding it. In the first, we write about the frictions that are brought into being and that play into the ways tools like BMA are designed and implemented. In the second view, we turn to the actual use of the tool and how the frictions arising from the different perspectives can be seen to enact a multiplicity of meanings. The last of the three views will focus more on the design of BMA’s user interface (UI) and represent a greater shift towards an analytical orientation that locates ourselves in the acts of building the tool and actively intervening in scientific ways of doing and knowing.
Our attention, then, will be on the intimate relations between a sophisticated computational tool, its design and use, and ways of knowing. Emphasised will be on the ways the unique properties of BMA entangle with and in biological ways of knowing and—we say this with caution—ways of being. As MacKenzie and McNally richly phrase it “worlds [are] made through the superimposition of different repetitions, aggregate worlds artificed in encounters with myriad multiples, worlds whose performative excesses undo or unmake identities as much as they make them” (ibid.). Ours will be a concern for how to better countenance such worlds, how to take their enactments seriously whilst imagining other productive and generative possibilities.
Before moving on to describe BMA and the details of its implementation and use, it seems appropriate to offer something of the context in which this work has emerged and our involvement in it. The BMA project has been set in a corporate lab in Cambridge (UK) that’s research themes fall almost exclusively under the rubric of computer science, e.g., networking, machine learning, human-computer interaction, etc. The exceptions to this work consist of research areas or projects that are in some way related to technology and computing, but are motivated by disciplinary programs outside of computer science. Such areas of research include environmental science, synthetic and computational biology, the sociology of technology and design.
The work presented began in this research lab’s Programming, Principles and Tools group, a group generally interested in theoretical aspects of programming abstractions and languages, and the tools used to manipulate them. Two of the group’s members, a cell biologist and computer scientist (along with external colleagues also in biology and computer science), had used formal methods techniques usually applied for verifying software and hardware code to successfully model stability in gene regulatory networks (Cook et al., 2011). The tool, however, relied on the manual entry of variables and a knowledge of programming to define variable relationships and execute the model checking algorithm. In short, it provided little in the way of accessibility for the kinds of biologists the tool was envisioned for. This led to the formation of the group tasked with building a UI for the tool that would be intelligible to the target users. In all, at the time of writing, the group consisted of a core team of nine members from biology (2), computer science (2), social science (2), design (1) and software engineering (2). The authors of this paper make up part of this assembled group⁵, and include those who built the original version of the tool and those contributing skills in user studies and design.
The materials used in this article are taken from a design phase spanning eighteen months in which we regularly attended group meetings to discuss the tool’s design. As well as these discussions, the following will make use of preliminary one-on-one interviews we held to introduce biologists to early iterations of the tool, and the use of the tool by two non-team members for their own research. While this kind of design-led work may be thought of as one step removed from the actual application of computation in biology, it does offer an extended and, as we’ll show, fruitful opportunity to witness the work of bringing computation and biology together. Moreover, it provides a way, as we will come to later, of placing ourselves amongst the troubles, of using the disciplinary variety to unsettle, disrupt and ultimately reimagine how computation intervenes in scientific practice.

Top-down Structural Modelling in BMA
Backtracking a little, to offer some details of the approach to modelling underpinning BMA, it could probably go without saying that computational modelling has offered a compelling way to manage the quantity and complexity of data observed in biology and, specifically, gene regulatory networks.⁶ The points have been made well elsewhere that in silico techniques offer ways of making abstractions and inferences that obviate the need to manually work through every possible case of a problem (and resort to time consuming and costly experimentation in the lab). Such techniques, though, can approach the problem of complexity and veracity in different ways. Although over simplifying things, a common way to categorise them is into bottom-up functional or top-down structural approaches.⁷
The bottom-up functional approaches build models around parts or components of a system understood to have biological functions. Ostensibly, the functional model represents the way a biological organism works or functions—it simulates the biology. So model parts may be cells, genes and/or proteins and the model may, for instance, represent the signalling pathways between them. By necessity, there are omissions, simplifications and abstractions made in the models, but the broad aim is to instantiate a one-to-one mapping with the elements of the cellular system and the biological relationships between them.
Top-down structural techniques employ a significantly different meaning of model. Models may or may not have an immediate correspondence to biological elements and their connections. What determines their structure is the computational technique applied—in a sense how the code or program is run to produce them. That is, the structure represents the way particular relationships between entities are formalised and evaluated in programmatic terms. A model may thus compute a proof, where the relations between a biological system’s elements are systematically tested against predefined criteria. Rather than simulate the biology, the model is structurally organised in terms of how the analysis is computed or executed.
BMA is an example of this latter approach. The computational underpinnings of the tool run what is known in computer science as a symbolic model-checking algorithm to prove whether the model achieves stabilisation. Stabilisation here refers to the cell-fate of a cellular system or network. It specifies whether that network has reached a stable state such as homeostasis or repeated cycles in cells. This cell-fate determination proves to be a powerful concept in computational biology as it enables biologists to refine their understandings of normal development processes as well as occasions where these go wrong, such as disease and cancer. So, for example, as we will go on to detail, BMA has been used to model cell-differentiation in blood. The first step to this has been to determine whether the structural arrangement of the cells and proteins drawn out in the model achieve the stable state exhibited in healthy blood cells. With the model confirmed against the reported results in the literature, the work has involved introducing various structural changes that might make the model more or less stable to perturbations. For instance, experiments have been run to test what might be done to lessen the possibility of the cells becoming unstable and replicating a leukemic pattern of cell differentiation. At stake in this case is one, the veracity of the model and, two, the model’s value in testing hypothetical therapeutic interventions to cancers such as leukaemia.
The innovation here is that BMA is able to prove stabilisation for highly complex models that, in structural terms, may have an infinite number of configurations or states. To work around problems of scale and complexity, BMA evaluates symbolic sets of the large and potentially infinite state space. Furthermore, rather than analysing the whole system, it answers questions about discrete pieces such that stabilisation is established as a composition of smaller mathematical arguments. In effect, BMA’s analysis results in a quick discovery of system components that take initial steps towards stabilisation and then finds the mechanism by which other components follow that lead. It is this that defines the tool’s approach as top-down. The testing of the configurations and sequential path through them is determined not by their biological characteristics per se, but instead by the way BMA’s underlying algorithm works.

View #1: Frictions in Building a Computational Tool
The computational proof that underpins BMA has been more or less complete since 2011 and shown to successfully replicate the results observed in laboratory experiments with mammalian skin cells and Caenorhabditis elegans (c. elegans) development (Cook et al., 2011). It is from this early implementation of the tool that the current group formed to design a graphical UI. To this end, we have designed a web-based front-end to support, one, the construction and manipulation of biological networks (Fig. 1) and, two, the execution of the proof and presentation of the results (Fig. 2). (For details of the UI see Benque et al., 2012). Although some sticking points persist, the features we’ve designed to achieve the first of these steps have reached a relatively mature stage of implementation. In preliminary trials, they have been straightforward to use and welcomed by users familiar with graphical layout applications such as Microsoft PowerPoint and Adobe Photoshop.

It is the tool’s display of the results that has been more problematic and that we will consider in more detail here. The most recent complete implementation runs the analysis with the straightforward selection of a ‘proof’ button in the tool’s interface. However, the display of results merely indicates whether the network has stabilised (green highlight) or, if there is instability, which network elements have failed to stabilise (red highlight)(Fig. 2). To add to the paucity of this visual information, the red highlight may also indicate the analysis having stalled or “timed out”. This is because the output from the proof originally treated the timing out of the analysis as equivalent to instability. Thus the tool effectively produces a binary output for each element in the model, representing stability or instability. Biologists responding to this have been confused by these outputs, unclear about what the results convey about a biological system and how they might be applied.

Referred to, collectively, as the ‘proof mode problem’ by the project’s members, the issues with presenting the results of the analysis have been revisited throughout the work. In design meetings, the algorithm underlying the tool has had to be repeatedly explained in order to decide how the results might be displayed and what other meaningful information could be provided to users. At the same time, a host of different designs for representing the proof and its output have been proposed and rejected.
Amongst the project team, the protracted discussions have, time and again, resorted to, on the one hand, the lead biologist struggling to understand why the biological processes can’t be represented and, on the other hand, the computer scientists explaining that the computational approach employed doesn’t allow for the simulation of biological processes. It isn’t that either side is unaware of the constraints. On the contrary, there has been a high degree of understanding of both the biology and computational workings from both sides. At issue is the seemingly intractable problem of representing the tool’s analysis in a way that is meaningful and useful to biologists.
It is the work at the interface that has surfaced the specific troubles here. By trying to quite literally materialise the multiple perspectives in the UI, what the design discussions have revolved around is an intrinsic tension in developing top-down structural approaches to modelling. Specifically, the repeated issues raised in trying to solve the proof mode problem appear to hinge on the movement from a computational formalism to the interface—in making-material computation. This materialising works draws in the multiple issues at stake: the computer scientists seeking to make highly complex phenomena susceptible to a computational logic; the biologists needing to see and work with recognisable biological processes; and design’s role in encoding both these standpoints in a visual/tactile abstraction. The struggle is seemingly with the mismatch between the standpoints, and the apparently essential differences between them. Certainly much has been said about how computation enforces a fundamentally different (and impoverished) understanding of scientific phenomena, and in particular biological life (cf. Giere, 2009; Guala, 2005; Krohs and Callebaut, 2007; Morgan, 2005 ; Stevens, 2011).⁸ Yet below, we want to show that this essentialising view is troubled in the actual use of BMA. Although the inclination is to slip into an essentialist frame (and this is certainly something those of us designing the tool have done), a certain pragmatism has been adopted by those using the tool. ⁹
For users, the emphasis has been on ‘further working things over’ in the back and forth work of biological modelling and experimentation (for a similar point, see Keller, 2000). Although it may seem an awkward way of phrasing it, this—we want to suggest here—reflects an ‘ontological impartiality’¹⁰ on the part of the tool’s users. Effort is put into making progress by drawing on a range of software tools in an assortment of scientific activities. Rather than representative of strong epistemic standpoints in themselves, the tools appear much more to be entangled in forms of knowing-in-progress, the practical ‘back and forth’ of working things out. It’s this pragmatic attitude towards BMA (alongside other tools)—and apparent fluidity towards epistemic and ontic forms—that we’ll later show has offered us a different way of approaching the proof mode problem. In short, it has presented the possibility of preserving the differences and tensions present in a tool-in-use and aiming to see this multiplicity as productive.

View #2: Multiplicity in Tool Use
The view that follows is developed from the first attempt by a non-member of the BMA team to use the tool, intensively, and over an extended period. Two different case studies of this kind have been undertaken so far, but the first of these, led by a MSc. student, Lucy, presents the most discussed amongst the team and well-documented example to date.
Lucy’s masters studies fall within a wider program of work at Cambridge University’s Cambridge Institute for Medical Research (CIMR) in which they are applying an “integrated approach” to determining the regulatory networks responsible for blood stem cell development. In biology, blood cell development or haematopoiesis constitutes one of the paradigm cases for studying stem cells and their peculiar capacity to both self-renew and differentiate into other cell types. A considerable literature therefore exists on the subject and there is plenty of scope for mining extant results and for cross-validation. Lucy’s use of BMA represents a continued effort to incorporate computational techniques into CIMR’s integrated approach—alongside other techniques such as in vivo experimentation and high-throughput sequencing—but also serves as a test case for, one, confirming BMA’s capabilities for modelling known biological phenomena and, two, determining whether the tool provides the basis for extending know-how in this discrete problem area of biology.
With respect to the first of these latter two objectives, Lucy’s original aim was to determine whether a regulatory network of transcription factor proteins and their interconnections, modelled in BMA, exhibited blood cell behaviours observed in the laboratory. Although the number of proteins in blood cells is known to be in there thousands, a review of the literature had identified thirteen transcription factors as crucial to blood cell differentiation—as their absence precluded normal blood production—and these formed the basis for constructing the network. Also incorporated were the complex array of promoting and inhibiting connections, and ‘qualitative’ indicators of the expression levels the proteins could vary between (e.g. 0-1 = low to medium, or 1-2 = medium to high). In combination, these interconnections and levels define the transcription factor proteins that can communicate with each other and the degree of influence they have over each other. Lucy’s use of BMA was to assess whether this network of proteins, connections and value ranges produced a model that was self-contained and did indeed reach a stable state.
With respect to the second objective, Lucy’s hope was that the introduction of perturbations into the BMA model might provide the basis for new hypotheses to be tested in the laboratory and ultimately new understandings of blood cell development. For instance, Leukaemia is known to be associated with the knockouts of particular transcription factors. The modelling in BMA was seen as a means of reproducing these knockouts and testing counterbalancing interventions, thereby hypothesising about therapies.
Lucy’s first problematic encounter with BMA was in configuring the transcription factors and connections in such a way that the regulatory network could be executed, computationally. With her initial attempts to compose and test the model, she found the tool’s analysis repeatedly timed out. With help from the team’s computer scientists, this was discovered to be because the connections she’d defined between the proteins were too literal and consequently had led to a complexity that was too demanding for the tool. The details behind this are unnecessarily technical here, but it is worth noting that to successfully test her model, Lucy needed to change the way she approached modelling and further abstract the structural configuration to conform to a notion of a model expected by the tool. As Byron, one of the team’s computer scientists put it, “she didn’t [initially] use it in the spirit it was written” and this necessitated a change in approach with the “right” structure of modelling in mind. The biology, in effect, had to be re-configured, structurally, to be ‘readable’ in computational terms and this required a change in mind-set—or “spirit”—on Lucy’s part.
We begin, here, to get a concrete sense of the frictions that can arise when modelling biology using computational techniques and specifically when a top-down structural as opposed to bottom-up functional approach is applied. Such frictions further manifest themselves in other apparent limitations to the tool. Although Lucy was eventually able to test the blood differentiation model using BMA and prove it stabilised, she found a severe limitation of the tool was the way it accounted for (or, to be more precise, did not account for) the progression of the biology over time. Quite simply, the tool does not model time. Indeed, it intentionally avoids doing so. To handle highly complex cell systems, and work through an inordinately large number of possible states, BMA, by design, avoids the need for temporal simulation. In Byron’s words:

“So we’re not running the system; we’re more making an argument at a level that is higher than basic time… We just start thinking about how the system is configured and start making logical inferences that are valid about the behaviour…”

Here again we are confronted by peculiarities of the top-down structural approach applied to model checking in BMA. The “logical inferences” that are made are derived using algorithmic formalisms, not properties purely of the biology and specifically not employing any idea of temporal progression of cellular organisms. In the case of Lucy’s blood cells, the proof did not model the five stages of cell differentiation observed in in vivo experiments, nor did it assume any starting points or complete pathways intrinsic to the biology. In simple terms, it took into account the range of variation and tested locally (and algorithmically) defined sets of connections. Nir, another of the team’s computer scientist, attempts to explain this:

“The way I think about [these] models is that they capture all points in time […] So in these kinds of models there is no element that says, well, I’m allowed to refer to my watch and change my behaviour according to time […] I’m constructing here a static picture of how they change for every possible time and every possible value.”

Critical here is that something seen as intrinsic to biology, time, is not accommodated in the approach to modelling used by BMA. Even in computer simulations of biology, the problem of modelling a “time-ordered sequence of states” is taken as given (Parker, 2009: 486). But in BMA the continuous and time-dependent properties of biological organisms, conventionally represented in biology using differential equations (Keller, 2002: 250), are quite simply absent. Conveyed by Nir is that the very power of the tool is achieved because it avoids having to work from any estimated starting points (that could be error-prone) and instead checks every possible state. The trouble is this extraordinary capability of the software surfaces problems at the interface. Lucy points to it as a source of confusion in explaining how she first imagined using the tool and the actual implication of BMA’s approach to modelling:

“We weren’t really sure what was going to happen initially. We were going to try and get it to go from one start point to the next and then through the stages individually but we couldn’t really do that once we’d abstracted everything so then we had to find another way of looking at the different points…”

She goes onto explain:

“We ended using a program based on [the model] in Excel – that Nir created – because a lot of the time it’s not actually the end point that’s most interesting, it’s how it got there and the intermediate stages—especially for this project.

Lucy describes the use of a workaround for the tool’s incapacity to simulate the temporal changes within the blood cells. Having proved stability using the tool, she had Nir help put together an Excel table so that she could manually enter and test values in her pared-down model. This enabled her to see, from predefined starting values, how the model progressed—in effect she’d found a means of (re-)introducing and simulating biological time and stepping through what are recognised to be the five stages of blood cell differentiation.
Once again, the use of BMA appears to exemplify the kinds of fundamental breakdowns that can occur between the representational forms considered intrinsic to biology on the one hand and afforded by computation on the other. Lucy is required to find a solution outside of the BMA tool to observe cell-change over time, even if the temporal delineation is crude. Certainly, this appears to give substance to the essentialist framing of biology. With such a frame, the frictions appear fundamental to the ways of knowing—computation relies on an impoverished and in some cases misleading representation of biological function and is thus a step removed from what can be known scientifically about biology (again, see Giere, 2009; Guala, 2002). Even if not dealt with explicitly, cell-change (or ‘cell-fate’, as it is known in the business) is tied to the progression of time. Experimentally, biology and time are entangled with one another; a commitment to time is, if you will, inherent in biological work at the ‘bench’ where experiments are conducted over time and through apparatuses and measuring devices that perform as well as operate in time. In modelling, time may be associated with different phenomena and thus treated in quantifiably different ways but the underlying principle is that biological organisms are to be understood with respect to some absolute measure of time. Thus, one could go so far as to say the computational modelling in BMA is performed as a second rate player in the practices that constitute scientific knowledge making and discovery because the frictions point towards a fundamental distinction between the practices of computational and ‘real’ meaning making. Lost is a biological, normative notion of time.
And yet the practice performs a very different picture. Unsurprisingly perhaps, rather than insurmountable, such frictions on the ground seem to be treated as pragmatic ones (at least in the case of BMA). Far more important to the tool’s potential users—users such as Lucy as well as the others we’ve interviewed—has been what might be thought of as its value in practice. Lucy comments on the immediate value of BMA lends some initial support to this:

“[The tool] confirmed that there weren’t any crucial links missing as well and that they weren’t the wrong way round cause when we tried switching them it went completely wrong.”

So the tool provides a quick if not completely fool proof way of assessing a model’s functional connections. Also, Lucy explains, it sits within a more intertwined set of practices of judgment, understanding and iterative modifications to the model:

“It is interesting cause you see which ones don’t stabilise … you have to then go back and look at the biology and see if that is interesting […] [and if] we’ve missed some connections… Also because we are only using the 13 genes and there are hundreds actually involved in the process like sometimes it would be useful to have other inputs but that’s a biological issue so we have to go back and say what is stopping that from stabilizing and it’s often because that particular protein is also regulated by something else.”

Lucy may seem to be appealing to a realist idea of biology as something one goes back to and looks at, but we take her thoughts to be indicative of a working up of biological reasoning for the pragmatic purposes of solving problems.
Such pragmatism evidently involves dealing with the limitations of what is known and working with tools that enable one to “go back” and test out new or alternative possibilities. We find modelling tools such as BMA subsumed into an assembled “machinery of seeing” (Amann and Knorr Cetina, 1988: 140) or “reasoning machinery” (Rheinberger, 1997: 20) in order to produce the object of study. This pragmatic attitude taken towards them, particularly in biology, confirms what others have observed in the history and philosophy of science and science studies (Law and Mol, 2002; Keller, 2002). Furthermore, we want to argue, it indicates an equivocal stance taken towards what might be construed from afar—or above—as frames with different epistemological bases. As Lucy suggests, her motive is really to be able to revisit the model and/or the biology and test out different ideas, to expand what is known. She appears relatively disinterested in whether the tools she uses are built on or result in inconsistent epistemological frames. Instead, she fluidly moves between seeing her objects as either theories-in-the-making or tools (Keller, 2002).¹¹ In short, a multiplicity of views onto the data are enacted in use and appear able to co-exist, more or less simultaneously.¹²
So, situated in use, BMA could well be recognised as a source of conceptual difficulties (as it has by the project team in their repeated attempts to resolve the proof mode problem). Moreover, these difficulties or frictions are manifestly born out in the coming together of computational and biological techniques and the representational forms they allow for. However, the difficulties, in practice, are centred on getting the results to make sense in practical terms, in short, in using them to determine “what to do”, a way to move on. Thus, moving between the various software representations of biology, Lucy was able to ask more questions about the model represented in BMA and to suggest changes.
Of particular relevance here is how we might understand BMA as a software tool. Seen alone, as a tool that figures biological phenomena with respect to computational formalisms, it appears an object vulnerable to conceptual difficulties. However, situated in use—practical use—we see it, as far as possible, being implicated in and giving shape to what Amann and Knorr Certina refer to as “a basis for a sequence of practice” (1988: 138); that is, contributing to “the work of seeing what the data consist of” (ibid.) and, particularly for BMA, ‘what to do with what is seen’.¹³ By interleaving BMA’s results with a temporal representation in Excel, for instance, the user can see the analysis introducing a way to interrogate and further augment a continually evolving ‘picture’ of cellular development. Again, the fault lines seem not to hinge on the epistemological or even ontological consistency of the data—a strict notion of what is real, or the coherence of the techniques used to produce and represent results. Rather it is whether they enable a trajectory of action and interpretation.
The application of software tools such as BMA seem, then, to be something fairly characterised in terms of a processual moving on. True, for BMA there have been some significant conceptual difficulties surrounding how networks are treated and particularly how time is accounted for. The relationships between the computational formalisms, the UI and use, are not at all pre-determined or fixed, however. So, with BMA, the difficulties are far from the unassailable frictions seen from an essentialist viewpoint. Instead, step-by-step, things get drawn together, compared, contrasted, reworked, etc.; the outcome is an interactional accomplishment, one that emerges from a working with and through the (in-)stabilities and frictions. For software, then, the lesson here appears to be that we come to understand computational tools not as cementing forms of knowing and doing, but rather in how they are entangled in processual relations through practice, and how these relations enact possibilities for moving on.

View #3: Moving On
Turning to the design work running alongside the early deployments of BMA, in this third and last view of the tool we will build on this idea of software’s capacity for new relations. We’ll show that the work at the interface can give shape to some implications of a different and arguably more substantive nature that both complicate but also offer a theoretical foundation for a ‘moving on’. Our aim here is to make room (albeit narrow at this stage) for actively intervening in science, for seeing frictions not merely as consequences of contradictory representations, but a beginning for a generative intermingling with practice—for, as Donna Haraway (2010) evocatively phrases it, “staying with the trouble”.
From the outset of designing BMA’s UI, the apparent incongruity between the computational workings and the biological processes have (as we’ve already commented) kept the team coming back to questions concerning how aspects of the analysis could be revealed to the user and, in particular, how a representation of cell-development over time might be incorporated in the tool. The proposal that has been repeatedly revisited to offer a solution to this has been to visualise the progression of the proof—that is, display to the user some representation of the proof progression over time, ‘proof time’, so to speak—as opposed to ‘biological time’.¹⁴ The challenge in taking this decision has been in how to reveal to the user that a distinctive kind of time is being referenced here, one likely to be unfamiliar, disruptive even, to biologists.
At first glance, such concerns with BMA’s interface may themselves seem to be purely pragmatic ones to do with standard problems associated with UI design. However, this work of implementing the UI brings us back, once again, to questions of knowledge making in science and specifically the interdisciplinary frictions raised by bringing software design, computation and biology together. The proof mode problem offers a case in point where, seen from one viewpoint, it is all too easy to slip into questions about what representational forms are more or less real and, from another viewpoint, how the ontological tensions can hinder scientific practice.
Although engaged in vastly different realms of scientific life, two relatively recent books have been particularly helpful in thinking through this tendency to slip into essentialist readings of the tool and the tensions that are enacted in doing so. One is Science and an African Logic (2001) by Helen Verran and the other Meeting the Universe Halfway (2007) by Karen Barad. Both present an analytic frame in which knower, knowledge and thing (matter) are inseparably entangled and located within on-going, processual practices. They contribute to a project that is concerned not with whether scientific (or for that matter indigenous) ways of knowing have a special or privileged right to truth claims or reality, but rather how knowing is something enacted through entanglements of people and things in action.
Verran weaves her way around and within the muddy separations between relativism and foundationism (the latter being, for our purposes, akin to realism). She disavows both by locating herself “inside” the acts of ordering and knowing. In her own studies of Yoruba-speaking children in Southwestern Nigeria, she observes the messiness of experimentation and the energy she (the experimenter) has invested in putting things in place. This is to understand ‘realness as emergent’ (2001: 37), always subject to and entangled in an unfolding assemblage of things being brought into relation to one another. By examining the unfolding controversies in quantum physics, Barad helps us to make sense of the apparatus vis-à-vis these ‘relational achievements’. The apparatus (or the scientific tools) are inseparable from the experiment, experimenter and phenomenal world, so that their “intra-action” are all assembled in what, exactly, the phenomenon is. “Every measurement involves a particular choice of apparatus, providing the conditions necessary to give meaning to a particular set of variables, at the exclusion of other essential variables” (2007: 115). The collective apparatus of observation—the tools, the scientist, the phenomenon, etc.—are thus always and unavoidably implicated in what is observed (and not observed) and consequently what is known—together they perform the ‘cut’. This Barad argues is not anti-realism (nor a relativism), but ‘agential realism’. As with Verran, there is a recognition that what is real is actively brought into—or performed in—the world; through the use of tools, phenomena are in a continuous state of becoming. These are the positions that help to define a “diffractive methodology”, a methodology that recognises that our practices matter, that we are, with no way out, accountable for the worldly configurations we enact.
Returning to BMA, what these arguments help to refine is an alternative conception of the proof mode problem and how to approach it vis-à-vis design. They help, conceptually, to see top-down structural tools such as BMA as new ways of interacting with and enacting biology, and thus ‘seeing’ the phenomena anew. If computational tools are thought not as lenses onto a static phenomenal world, a ground truth or “ordered ground” (Law and Lien, 2012), but instead part of the always-emergent assemblage of things that constitute the “intra-action” of the experiment, we begin to see how the proof mode problem is not merely something to be overcome by re-introducing some notion of ‘real’ or ‘natural’ biological processes. Rather, it becomes a means of enabling one particular relational achievement over (or as well as) another. A challenge becomes how to make such unfolding and emergent relational achievements materially possible and intelligibly open, so biologists can ‘move on’ in their work.
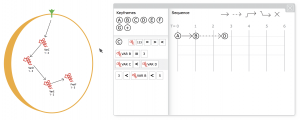
Let us turn to one final feature of BMA—that is in development in an unreleased version of the tool—to consider what this productive reimagining of the frictions might mean in practice and what might be at stake for computational biology and those designing software tools. To better accommodate the iterative, hypothesis-driven experimentation in biology, the computer scientists in the BMA team have implemented a new ‘bounded’ technique for model checking that allows smaller parts of the model to be tested. The technique enables users to step through the model checking process (in a limited fashion) and test out particular hypotheses, rather than merely being shown the final results. In effect, this introduces a notion of temporality to the tool and thereby addresses at least one of the central concerns of the proof mode problem, the absence of a sequence of events that might help as user to interpret the results. This addition to BMA works by allowing the user to specify a start and/or end state of a subset of elements in a cellular network and, subsequently, to view the corresponding sequence of events.¹⁵
Again the computational details of this bounded model checking are unnecessary here. Relevant though is that the sequence and number of states taken to reach an endpoint are determined algorithmically. In order to achieve results quickly, the technique deduces which variable values are likely to change next and limits its search for subsequent states accordingly. Therefore, the best that could be said of the technique is that it provides a possible example of a bounded sequence of events in a cellular system. Manifestly, the output is partial: alternative sequences from a given starting point may also be viable but not shown; individual step changes may happen in sequence but may also occur in parallel; only smaller parts of a larger network can be analysed; and there is no way to determine the relative proportion of time between steps, let alone the changes vis-à-vis any normative notion of (biological) time. So, although the team has gone some way towards better situating the tool’s results in a ‘sequence of practice’—one in which biologists might hypothesise and experiment with subsets of a larger model they know either succeeds or fails to stabilise—the algorithmic properties do impose further potential anomalies.
For the team, the recognition of a pragmatism on the part of its intended users is being treated as an opportunity to take quite a different approach to this new output to the analyses. We have experimented with juxtaposing the outputs from different types of analysis, placing them side-by-side (Fig. 3). Sequences, labelled in tabular rows and columns (not unlike Lucy’s Excel spreadsheet), are set against the graphical representation of the cell network. The distinctions between them are intentionally blurred, however. Interacting with one representation alters the representation of the other: change a link between nodes in the diagram and the sequence table updates, change a value in the sequence table and the corresponding part of the graphical representation is updated. Thus, in this unfinished state of BMA’s design, questions are purposefully being invited about where many things begin and end. Questions hang on the distinctions between biology and simulation, biology and algorithmic execution, and broadly on representation and intervention. Even the cornerstone of the tool, stability, comes to be a concept hanging in the balance; in these more recent stages of design, Ben, another of the biologists on the team admits an uncertainty about the distinction between stability in the biological system and what he calls “correctness” of the model. As a key player in determining BMA’s use and its design, even Ben struggles with what precisely is being proved stable using the tool.

Frictions then remain. Unsurprisingly, a fix to problems brought into being through the elisions of biology and computation overcome some limitations, but retain and introduce others. The team’s attempts to remedy the proof mode problem, or at least partially address it, keep the trouble going. As the work progresses, the questions asked of the biology come to be computational-like and the computation is refigured, as best it can, as biology-like. The relations are so entangled that it no longer seems to be a matter of disambiguating the biological from the computational; the two are mutually enacted in the tool’s use. Furthermore, the tool pushes back on the team. The problem(s) are figured and re-figured so that, as a team, we are forced to ask ourselves very different questions that weren’t originally intended in the tool’s design or use. In BMA, where do the stabilities and sequence of events reside? Are we performing and seeing some property of the computation here or of the biology? Might they be entangled in the hybrid, our hybrid?
These are the material practices and intra-actions that matter for Barad (2007) and Verran (2001). We see how the apparatuses configured to see and make sense of scientific phenomena enact worlds of knowing and sometimes bring multiple worlds together, enacting difference. As a tool, BMA and its incremental additions cut through and circumscribe particular ways of biological knowing. And these cuts and circumscriptions enact phenomenal worlds in which biology is progressively understood and known to be something that operates in state-like ways; that can be reducibly ordered to temporal sequences; and that is calculably stable. However, if the biology achieves stability, these worlds do not. Within them, the phenomena, (machinic) apparatuses, human actors, etc. repeatedly perform frictions in their ongoing entanglements. Biology-as-states and biology-as-a-temporal-sequence can’t be easily reconciled, and users run into moments where the differences cast doubt on seeing the machine from the biology and the biology from the machine.
The diffractive methodology here is a productive ‘moving on’. It is to see the trouble—the differences and frictions—as possibilities for intervening in the “specific material configurations of the world’s becoming” (Barad, 2007: 91). It is to unsettle the determination of stability, in recognition that the “practices of knowing are specific material engagements that participate in (re)configuring the world” (ibid., emphasis in original). This is what we take to be a productive interjection into our design of BMA and hopefully an exemplar of how we might rethink the relations enacted through software tools and what it means to design them. While sensitive to the intelligibility of the tool’s UI, our efforts have been to leave enough space for uncertainty in such a way that all things don’t, if you will, add up. Indeed, the inconsistencies or frictions are treated not as some troublesome problem with the tool and its types of analyses (as though these were separate from the phenomena). Instead, they are seen as opportunities for representing multiple figurings of phenomena—a multiplicity—so that the tool’s users might just stay with the trouble and discover routes for moving on. That is, the frictions, apparently rooted in disciplinary divides, have come to be seen on the team’s part as opportunities for opening up the sequence of practices, and potentially for different or new ways of knowing. Embedded in the tool is an idea of scientific ways of knowing not passively waiting to be found in “objects-ready-made” (Verran, 2001: 152), but contingent and situated in practice.
Crucially, the implication here is not just to imply a view from outside, remarking critically on and then intervening in the enacted relations and productions of meaning. Nor is it to suggest we have discovered some optimal way of helping our users to move on in their work. More than this, our efforts represent an attempt to locate ourselves in those very same acts of moving on. By working at and on the interface, we locate ourselves in that collective apparatus of observation in no lesser way than the biologist using BMA. Revealing the multiplicity of meanings is to understand not only how we might introduce room for new ways of seeing and doing for the tool’s users, it is an attempt to own up to (in a manner of speaking) the interventions we, in designing the tool, are party to. This is an attempt to openly participate in Teil’s “regimes of existence” (2013), but in such a way that (some of) the machinery might be made visible precisely because it is left open and unresolved.
Thus, the reference to moving onwards has its double meaning here where value is found not only in the multiplicity of meanings for our biologists (as if we were teaching them something they didn’t already know). The very same initiative is an intervention in our own practices of accounting and doing. To borrow Verran’s (2001) phrase, it is a “collective going-on”. It is to engage with the science studies and feminist readings of (quantum) entanglements in generative forms of knowing (Barad, 2007; Haraway, 1991; Kirby, 2011; Lury and Wakeford, 2012)—to participate, actively, in the always already mutual enactments of knowing and to take “responsibility and accountability for the entanglements “we” help enact and what kinds of commitments “we” are willing to take on” (Barad, 2007: 382).

Conclusion
In conclusion, this work can in many respects be seen as an example of ordinary scientific practice and knowledge making, and the concomitant interleaving trajectories of human and non-human agents (Latour and Woolgar, 1986; Mol, 2003). Furthermore, by engaging with contemporary theorising in feminist technoscience and the philosophy of science, as well as science studies, it elaborates on the new materialist or relational-materialist arguments that still appear to be in the throws of stitching together a shared movement, let alone agreeing on a common nomenclature (if such ambitions aren’t antithetical to the cause).¹⁶
For software studies, the hope is the work offers a deepening in thinking about computation and how, exactly, it surfaces in and entangles with scientific life and knowledge making. We’ve aimed to show how the formalisms and logic undergirding software and the software itself do much more than ‘represent’ worldly phenomena. Likewise, we’ve shed light on how computationally sophisticated software doesn’t just encapsulate or embody ways of knowing. The above illustrates how there are epistemics and ontics of algorithms, computation and software that are enacted at the interface of coding, design and scientific practice. Multiples are materialised at this interface, and knowings come into being through a working through of these multiples.
Beyond this explication of scientific practice and engagement with theory, our hope has also been to do something more. The aim has been to offer the possibility of interjecting in scientific practice. The materialist turn in STS invites such interventions in its recognition that “representations are not… pictures of what is, but productive evocations, provocations, and generative material articulations or reconfigurations of what is and what is possible” (Barad, 2007: 389). This places the onus on scholars not only to produce accounts of practice, but to also accept their active participation in them. Thus ours, to borrow Christie and Verran’s words, is “not… a move to the ‘outside’ of knowledge and the encounters in which it comes to life. On the contrary, … [it is] to learn how to work with tools that can make the move in the other direction, towards an infra-level of practices” (in press: 8). Ever-so modestly, then, with the “ever-ongoing necessity of care” (Mol, 2012), our hope has been to accept the invitation for the enactments of other “out-therenesses” (Law, 2004: 40), and to do so by being inside the troubled practices.
By designing at the interface (with tools, and between computation and biology), we’ve sought to show there is scope to provoke and, ultimately, introduce such out-therenesses from inside. BMA and other computational tools like it, stand as very different tools for interacting with biological phenomena, and thus provide the basis for different epistemic enactments. Because they offer different ways in which to work with and reflect on the biology, they open up the possibility of seeing and knowing it differently. The aim has not been to restrict ideas of biology so that they cohere to consistent epistemological or even ontological narratives, but allow for a multiplicity of knowings to be represented and intervened in. Design at the interface, in this sense, becomes one of the ways in which we as science scholars might “nudge programs of research” (Law, 2004: 40), be they in biology or otherwise.

References
Agar, Jon. “What Difference Did Computers Make?” Social Studies of Science 36, no. 6 (2006): 869–907.
Amann, Klauss, and Karin Knorr Cetina. “The Fixation of (visual) Evidence.” Human Studies 11, no. 2 (1988): 133–169.
Barad, Karen Michelle. Meeting The Universe Halfway: Quantum Physics and the Entanglement of Matter and Meaning. Durham: Duke University Press, 2007.
Benque, David, Sam Bourton, Caitlin Cockerton, Byron Cook, Jasmin Fisher, Samin Ishtiaq, Nir Piterman, Alex S. Taylor, and M Vardi. “Bio Model Analyzer: Visual Tool for Modeling and Analysis of Biological Networks.” In Proceedings of the 24th International Conference on Computer Aided Verification (CAV), 686–692. LNCS 7358, 2012.
Birch, Kean, and David Tyfield. “Theorizing the Bioeconomy: Biovalue, Biocapital, Bioeconomics or… What?” Science, Technology & Human Values 38, no. 3 (2013): 299–327.
Bowker, Geoffrey C, and Susan Leigh Star. Sorting Things Out: Classification and Its Consequences. London: MIT Press, 2002.
Carlson, Robert H. Biology is Technology: The Promise, Peril, and New Business of Engineering Life. Cambridge MA: Harvard University Press, 2011.
Cartwright, Nancy. “Models: The Blueprints for Laws.” Philosophy of Science 64 (1997): S292–S303.
Cartwright, Nancy. “Models and the Limits of Theory.” In Models as Mediators: Perspectives on Natural and Social Science, ed. Mary S Morgan and Margaret Morison, 241–281. Cambridge: Cambridge University Press, 1999.
Christie, Michael, and Helen Veran. “Digital Lives in Postcolonial Aboriginal Australia.” Journal of Material Culture 18 no. 3 (2013): 299–317.
Cook, Byron, Jasmin Fisher, Elzbieta Krepska, and Nir Piterman. “Proving Stabilization of Biological Systems.” In Verification, Model Checking, and Abstract Interpretation, 134–149. Berlin Heidelberg: Springer, 2011.
Cook, Byron, Andreas Podelski, and Andrey Rybalchenko. “Proving Program Termination.” Communications of the ACM 54, no. 5 (2011): 88–98.
de Laet, Marianne, and Annemarie Mol. “The Zimbabwe Bush Pump: Mechanics of a Fluid Technology.” Social Studies of Science 30, no. 2 (2000): 226–263.
Edwards, Paul N., Matthew S. Mayernik, Archer L. Batcheller, Geofffrey C. Bowker, and Christine L. Borgman. “Science Friction: Data, Metadata, and Collaboration.” Social Studies of Science 41, no. 5 (2011): 667–690.
Fisher, Charles S. “Some Social Characteristics of Mathematicians and Their Work.” American Journal of Sociology 78, no. 5 (1973): 1094–1118.
Fisher, Jasmin, and Thomas A. Henzinger. “Executable Cell Biology.” Nature Biotechnology 25, no. 11 (2007): 1239–1249.
Fujimura, Joan H. “Technobiological Imaginaries: How Do Systems Biologists Know Nature?” In Knowing Nature: Conversations at the Intersection of Political Ecology and Science Studies Knowing Nature: Conversations at the Intersection of Political Ecology and Science Studies, eds. Mara J. Goldman, Paul Nadasdy, and Matthew D. Turner, 65–80. London: The University of Chicago Press, 2011.
Giere, Ronald N. “Is Computer Simulation Changing the Face of Experimentation?” Philosophical Studies 143, no. 1 (2009): 59–62.
Goodwin, Charles. “Professional Vision.” American Anthropologist 96, no. 3 (1994): 606-633.
Guala, Francesco. “Models, Simulations, and Experiments.” In Model-Based Reasoning: Science, Technology, Values, eds. Lorenzo Magnani and Nancy J. Nersessian, 59–74. New York: Kluwer, 2002.
Hacking, Ian. Representing and Intervening: Introductory Topics in the Philosophy of Natural Science. Cambridge: Cambridge University Press, 1983.
Haraway, Donna J. Simians, Cyborgs, and Women: The Reinvention of Nature. New York: Routledge, 1991.
Haraway, Donna J. “When Species Meet: Staying with the Trouble.” Environment and Planning. D, Society and Space 28, no. 1 (2010): 53.
Hird, Myra J. “Feminist Matters: New Materialist Considerations of Sexual Difference.” Feminist Theory 5, no. 2 (2004): 223–232.
Keller, Evelyn Fox. “Models of and Models for: Theory and Practice in Contemporary Biology.” Philosophy of Science 67 (2000): S72–S86.
Keller, Evelyn Fox. Making Sense of Life: Explaining Biological Development with Models, Metaphors, and Machines. Cambridge, MA: Harvard University Press, 2002.
Kelly, Gregory J. “Research Traditions in Comparative Context: A Philosophical Challenge to Radical Constructivism.” Science Education 81, no. 3 (1997): 355–375.
Kirby, Vicki. 2011. Quantum Anthropologies: Life at LargeI. Durham, NC: Duke University Press.
Krohs, Ulrich, and Wemer Callebaut. “Data Without Models Merging with Models Without Data.” In Systems Biology: Philosophical Foundations, ed. Fred C Boogerd, 181–283. Amsterdam: Elsevier, 2007.
Lakatos, Imre. Proofs and Refutations: The Logic of Mathematical Discovery. Cambridge: Cambridge University Press, 1976.
Latour, Bruno, and Steve Woolgar. Laboratory Life: The Construction of Scientific Facts. Chichester, West Sussex: Princeton University Press, 1986.
Lave, Jean. Cognition in Practice: Mind, Mathematics, and Culture in Everyday Life. Cambridge: Cambridge University Press, 1988.
Law, John. After Method: Mess in Social Science Research. London: Routledge, 2004.
Law, John, and Marianne E. Lien. “Slippery: Field Notes in Empirical Ontology.” Social Studies of Science 43, no. 3 (2012): 363-378.
Law, John, and Annemarie Mol. Complexities: Social Studies of Knowledge Practices. Durham: Duke University Press, 2002.
Lury, Celia, and Nina Wakeford. Inventive Methods: The Happening of the Social. Abingdon, Oxon: Routledge, 2012.
Mackenzie, Adrian, and Ruth McNally. “Living Multiples: How Large-Scale Scientific Data-Mining Pursues Identity and Differences.” Theory, Culture & Society 30 (2013): 72–91.
MacKenzie, Donald A. Mechanizing Proof: Computing, Risk, and Trust. Cambridge, MA: MIT Press, 2001.
Mattila, Erika, Tarja Knuuttila, and Martina Merz. “Computer Models and Simulations in Scientific Practice.” Science Studies 19, no. 2 (2006): 3–11.
Merz, Martina, and Karin Knorr Cetina. “Deconstruction in a `thinking’ Science: Theoretical Physicists at Work.” Social Studies of Science 27, no. 1 (1997): 72–111.
Mol, Annemarie. The Body Multiple: Ontology in Medical Practice. Durham, N.C. ; London: Duke University Press, 2003.
Mol, Annemarie.. “Keynote Address: Textures and Tastes – The Future of Science and Technology Studies.” Presented at The Annual meeting for the Society for Social Studies of Science (4S)/EASST, October 17-20, 2012. Copenhagen, Denmark.
Mol, Annemarie. “Mind Your Plate! The Ontonorms of Dutch Dieting.” Social Studies of Science 43, no. 3 (2013): 379–396.
Morgan, Mary S. “Experiments Versus Models: New Phenomena, Inference, and Surprise.” Journal of Economic Methodology 12 (2005): 317–329.
Morrison, Margaret C. “Models, Measurement and Computer Simulation: The Changing Face of Experimentation.” Philosophical Studies 143 no. 1 (2009): 33–57.
Myers, Natasha. “Molecular Embodiments and the Body-Work of Modeling in Protein Crystallography.” Social Studies of Science 38, no. 2 (2008): 163–199.
Myers, Natasha. “Conjuring Machinic Life.” Spontaneous Generations 2, no. 1 (2009): 112–121.
Parker, Wendy S. “Does Matter Really Matter? Computer Simulations, Experiments, and Materiality.” Synthese 169, no. 3 (2009): 483–496.
Rheinberger, Hans-Jorg. Toward a History of Epistemic Things: Synthesizing Proteins in the Test Tube. Stanford, CA: Stanford University Press, 1997.
Rosental, Claude. Weaving Self-Evidence: A Sociology of Logic. Princeton: Princeton University Press, 2008.
Rowbottom, Darrell P. “Models in Biology and Physics: What’s the Difference?” Foundations of Science 14, no. 4 (2009): 281–294.
Schrader, Astrid. “The Time of Slime: Anthropocentrism in Harmful Algal Research.” Environmental Philosophy 9, no. 1 (2012): 71–93.
Sommerlund, Julie. “Classifying Microorganisms: The Multiplicity of Classifications and Research Practices in Molecular Microbial Ecology.” Social Studies of Science 36, no. 6 (2006): 909–928.
Stevens, Hallam. “Coding Sequences: a History of Sequence Comparison Algorithms as a Scientific Instrument.” Perspectives on Science 19, no. 3 (2011): 263–299.
Teil, Geneviève. “No Such Thing as Terroir? Objectivities and the Regimes of Existence of Objects.” Science, Technology & Human Values 37, no. 5 (2012): 478–505.
Tutton, Richard. “Promising Pessimism: Reading the Futures to be Avoided in Biotech.” Social Studies of Science 41, no. 3 (2011): 411–429.
Verran, Helen. Science and an African Logic. Chicago: University of Chicago Press, 2001.
Winsberg, Eric. “Simulations, Models, and Theories: Complex Physical Systems and Their Representations.” Philosophy of Science 68 (2001): S442–S454.

 

Notes