Subversive Witness: The Disruptive Influence of Bayes Theorem on Forensic Science

1. Introduction

Bayes Theorem has claimed an increasing number of applications and stimulated widespread interest, but remains largely studied in analytical terms as the preserve of statistics and probability theory. This article instead considers the significance of Bayes Theorem from the standpoint of qualitative social research. It draws upon conceptual resources from Science and Technology Studies to critically explore applications of Bayesian reasoning in forensic science.

Statistics and probability theory in general terms have received critical attention from sociologists and historians of science, with some notable arguments being made regarding the social construction of statistical objectivity¹. Minimal specific attention has however been paid to Bayes Theorem. One exception is Kruse’s (2013) ethnographic study of Bayesian reasoning in Swedish forensic science laboratories. Kruse argued that Bayesianism functioned as an ordering mechanism, which stabilised a particular form of intersubjectivity among forensic scientists by producing shared understandings and distributing responsibility for the production and interpretation of forensic evidence². These findings highlight the potential to consider Bayesianism more as a social phenomenon rather than simply a quantification of individual subjective belief. Kruse’s work moreover raises the question of whether Bayesian practices are best framed either as an outcome or means of social construction.

The use of probability theory, and Bayes Theorem in particular, has been of interest to forensic scientists and legal scholars for some considerable time, as discussed further in Section 2. The application of Bayes Theorem to forensic science has been claimed to provide a more robust epistemological basis for reasoning about evidence. This is particularly significant given criticisms of many forensic techniques, which have often drawn negative comparisons between forensic science and the so-called ‘pure’ research sciences³. While some of these criticisms have claimed a lack of systematic reliability testing, and raised concerns around provision for peer review, critics have also raised issues over the specific methods used in forensic analyses. For example fingerprint examination, often considered emblematic of forensic science, has been claimed to rely on a high level of subjectivity when comparing prints between those recovered at crime scenes and those taken from individuals. Critics have claimed that fingerprint analysis still often involves mere visual comparison of images in conditions which perpetuate bias⁴. Such criticisms have extended to other common forms of forensic analysis⁵.

In response, Bayesian methods have been developed in the interests of epistemological reform of forensic science. Bayesian logic has been incorporated into automated systems used to interpret biometric data, and has also been promulgated as a general framework for interpreting forensic evidence in the context of criminal investigations⁶. Bayesian frameworks enable differing interpretations, such as prosecution and defence arguments, to be considered in the same frameworks for evidential assessment and analysis. Such methods have been accepted as standard practice internationally⁷.

This article charts the emergence of Bayes Theorem in forensic science via two examples of its application. The first concerns the Case Assessment and Interpretation (CAI) framework, developed by UK forensic scientists to apply Bayes Theorem holistically to criminal investigative casework. The second example involves the development of Bayesian algorithms in systems used to interpret complex forensic DNA profiles.

These two examples allow the article to challenge formalised depictions of forensic Bayesianism, by addressing the epistemological and ontological lacunae to which hitherto unaware investigators may be exposed, or which alternatively may be concealed within Bayesian formulae. Rather than merely functioning as a linear means for mathematically evaluating hypotheses and for representing belief, this article demonstrates how forensic Bayesianism may either open up or render silent areas of ambiguity or uncertainty, raising questions for how western judicial systems control material witnessing.

The article proceeds as follows. Section 2 provides a historical outline of the application of probability theory and Bayes Theorem to western criminal justice and forensic science. Next, Section 3 introduces some key principles of forensic Bayesianism. Section 4 presents the two examples of forensic Bayesianism in the form of CAI and DNA interpretation technologies respectively. Finally, Sections 5 and 6 outline the possible wider implications of these findings.

First however a note on methodology. The article draws upon several years of research on forensic Bayesianism conducted by the author. This includes examination of scientific, legal and policy texts, and participant observation at numerous discussions over the use of Bayesian methods in forensic science and criminal justice. The article also draws on semi-structured interviews conducted with forensic practitioners involved in criminal investigative casework. The latter took place between 2006 and 2010. More recently however the author examined the status of forensic Bayesianism through participation in regular events from 2015 to 2023. This involved observing further scientific, legal and academic dialogue concerning forensic evidence, which took place at various seminars and conferences. This allowed the author to trace more contemporary developments and to compare them with older fieldwork.

2. Historical Overview

There have long been efforts to develop statistical methods for the interpretation of evidence, both during courtroom trial procedures and for forensic scientific work in particular. The legal scholar John Henry Wigmore, working in the early twentieth century, outlined what is generally regarded as the first holistic and systematic framework for the interpretation of evidence in criminal trials through articles such as ‘The Problem of Proof⁸].’ Wigmore viewed his programme as focusing on two distinct areas: the issue of proof in the general sense, ‘the part concerned with the ratiocinative process of contentious persuasion’, and the other that of admissibility, ‘the procedural rules devised by law, and based on litigious experience and tradition, to guard the tribunal (particularly the jury), against erroneous persuasion⁹.’ In his opinion, studies had exclusively focused on the latter in a manner that he felt to be detrimental to the progress of law. For Wigmore, notions of proof ‘in the general sense’ would remain invariant as the foundation for law, in contrast to admissibility, which he saw as ‘merely a preliminary aid to the main activity’ of proof, namely ‘the persuasion of the tribunal’s mind to a correct conclusion by safe materials¹⁰.’

Wigmore anticipated a move away from a concern with tradition in legal procedure, to a stance attuned to more avowedly scientific principles. He argued that legal professionals required instruction in what he called a ‘science of proof¹¹.’ Wigmore was however concerned that the potentially wide array of pieces of evidence, testimony, and arguments that could be involved in criminal cases could be overwhelming for reasoners. He also saw the need to avoid adducing disproportionate weight to individual pieces of evidence by privileging them over other evidence. Wigmore assumed the fallibility of human belief and dependence on ‘how fully the data for the fact have entered into the formation of our belief’¹², and argued that human reasoners could only comprehend multiple facts one after the other.

Wigmore set out to develop technologies to help judicial reasoners overcome the cognitive problems associated with case reasoning, such as bias, oversight or the unbalanced privileging of certain pieces of evidence against others. He also sought to highlight the types of interdependencies between pieces of evidence which could be identified, such as the ability of one form of evidence to influence the perceived level of accuracy or reliability of another. To this end he developed a graphical system to depict how advocates reason through a case. In doing so Wigmore aimed to provide a holistic and descriptive representation of how the reasoning processes in a case may proceed, and to map the processes of evidence interpretation from both a prosecution and a defence viewpoint.

Wigmore’s work is now acknowledged as an important contribution to evidence scholarship, but at the time it received little attention from academics or legal practitioners. The subject of evidence did however continue to be addressed by leading American legal scholars as the twentieth century progressed¹³. This included calls for greater import of statistics and probability theory into legal reasoning¹⁴.

Bayesian methods attracted attention from scholars based at university business schools, who were interested in how individuals made business decisions under conditions of uncertainty¹⁵. This research crossed over into legal studies through articles such as that of Kaplan (1968), which addressed the use of probability theory in court cases¹⁶ and the work of Finkelstein and Fairley (1970) who presented a Bayesian framework which they argued could establish the probative force of forensic evidence¹⁷. This research prompted renewed academic debate over the role of probability theory in law, which was seen to revive evidence scholarship¹⁸. The work of Wigmore was subsequently reappraised, notably by Tillers and Schum¹⁹, who saw the Wigmore chart method as significantly advancing understanding of what they called ‘discovery-related activity²⁰.’ They regarded the Wigmore chart method as assisting investigators to generate hypotheses by enabling them to view relationships between different pieces of evidence. Kadane and Schum (1996) would later combine Wigmore charts with Bayesian analysis in their re-investigation of the Sacco and Vanzetti case, which led to the execution of two Italian men for murder and was long seen as a possible miscarriage of justice²¹.

During the 1960s, a parallel discourse emerged more specifically within forensic science. In 1963, Paul Kirk, a leading figure in the US forensic science community, published a short article, ‘The Ontogeny of Criminalistics’, which effectively marked an attempt to define the scientific essence of forensic science:

‘The real aim of all forensic science is to establish individuality, or to approach it as closely as the present state of the science allows. Criminalistics is the science of individualism²².’

Kirk’s statement came at a time when there was an increased interest in the use of statistical methods in forensic science, which ran alongside debates among legal scholars. In 1964, a special session on statistics was held at a meeting of the American Academy of Forensic Sciences, which reflected the apparently ‘growing awareness of the usefulness of statistical methods²³.’ Charles Kingston, a student and collaborator of Kirk, published two articles concerning “Applications of Probability Theory to Criminalistics²⁴,” which discussed and put forward a number of probabilistic models for the assessment of Partial Transfer Evidence (PTE), such as toolmarks or fingerprints, and included an explicitly Bayesian model.

The Bayesian approach to evidential reasoning received further application through the work of the UK Forensic Science Service (FSS), notably via the research of statistician Dr Ian Evett, who worked with the distinguished Bayesian Denis Lindley²⁵. Lindley and Evett applied Bayes Theorem to PTE analyses such as glass and fibres, documented in a number of scientific articles²⁶. Evett saw Bayes Theorem as providing a solution to the apparently unique problems experienced in forensic scientific work, and argued that it provided a means of evaluating evidence in cases where the transfer of material had occurred from ‘criminal to crime scene²⁷.’

A group of FSS researchers, including Evett, subsequently developed the Case Assessment and Interpretation (CAI) model. CAI seeks to holistically apply Bayesian principles through a set of procedural guidelines to evaluate hypotheses formulated in relation to forensic evidence during criminal investigations. The example of CAI is described in more detail in Section 4.1, but first it is necessary to outline some key principles of forensic Bayesianism.

3. Forensic Bayesianism: Key Principles

Bayes Theorem involves updating beliefs given in the form of probabilities. An existing belief, given as a prior probability, may be modulated via Bayes Theorem to lead to a possibly updated or altered posterior probability. Here, Bayes Theorem takes the form:

Posterior probability (Probability of a hypothesis given evidence)
= Prior probability (Probability of hypothesis) × Probability of evidence given hypothesis

Or:$$P (H|E) = P(H) \times P(E|H)$$
Forensic applications of Bayes Theorem typically involve adapting this equation to allow the comparison of two hypotheses, relating to prosecution (\(H_p\)) and defence (\(H_d\)) arguments. Here the Bayesian formula generally takes the form:
$$P (H_p|E) = P(H_p) \times P(E|H_p)$$
$$P(H_d|E) = P(H_d) \times P(E|H_d)$$
The ratio \(P(E|H_p) / P(E|H_d)\) is the likelihood ratio (LR). LRs can provide an indication of whether a piece of evidence favours a prosecution argument \(P(H_p|E)\) or an alternative, possibly defence argument \(P(H_d|E)\). The generation of LRs can involve the formulation of pairs of corresponding prosecution and defence propositions:
LR = Probability of the evidence given a prosecution proposition
Probability of the evidence given a defence proposition

For example the analysis of a forensic DNA profile, involving a possible match between DNA recovered from a crime scene and the DNA of a potential suspect, can be evaluated through such a Bayesian framework.

A prosecution argument would assume that the suspect is guilty and thus would argue that, if so, the probability of a match between this individual and the crime scene profile is certain, thus a probability P(E|Hp) = 1. A defence argument on the other hand could seek to advance an alternative explanation, such that the crime scene DNA could have been deposited by a different individual who happened to share the same DNA profile. The probability that two individuals share a DNA profile is known as the random match probability. The kind of forensic DNA profiles routinely used in police investigations typically consist of collections of specific DNA patterns (alleles) found within specific parts (loci) of an individual’s genome, which is itself distributed within chromosomes found in most of the body’s cells. The type of DNA patterns may vary at each locus among human populations, and thus if several loci are analysed and typed, a profile can be generated which provides a distinctive if not necessarily unique pattern of data for that individual. The random match probability is calculated by estimating the relative frequency of each DNA pattern found at each locus within a human population, and multiplying these frequencies together in accordance with basic laws of probability, to estimate the probability that two or more people might share the same profile. While in practice the random match probability may be extremely low, it is considered an alternative explanation to the prosecution position. The random match probability can then be used to calculate LR via the Bayesian formula presented above.

Forensic Bayesian frameworks can be applied to other forms of evidence. For example, a shoeprint may be recovered from a crime scene and be considered potentially significant to an investigation. A suspect may be apprehended who is found wearing what appear to be shoes which match the print. In this scenario, investigators using a Bayesian framework would again consider two explanations: a prosecution hypothesis would assume that the probability of the suspect’s shoes creating the print to be p=1 under the assumption that the suspect is guilty of the crime under investigation. An alternative defence hypothesis could instead consider the probability that the shoeprint was created by someone else who happened to possess the same type of shoe. Formulating a probability estimate for the defence hypothesis could entail considering the relative frequency of the shoe type in a population. This might involve assessing whether the shoe is a commonly sold brand and/or size, (which could potentially involve seeking data on specific shoe sales in a certain area), or whether the shoe is a rare type or size. A rare shoe type might lead investigators to regard the evidence as more probative and to favour a prosecution hypothesis. If however the shoe type is found to be relatively frequent, it may lend greater support to the defence hypothesis by suggesting a reasonably high probability that the shoe print could have been created by someone other than the suspect.

4. Two Examples of Forensic Bayesianism

4.1. Case Assessment and Interpretation (CAI)

The interest in applying Bayes’ Theorem to forensic science was accompanied by an emerging view that the defining characteristic of forensic practice entails ‘the interpretation of[scientific] results in the individual context of each case²⁸.’ Authors of CAI expressly stated ‘the Bayesian view of evidence[to be] that it is not sensible for a scientist to attempt to concentrate on the validity of a particular proposition without considering at least one alternative²⁹.’ CAI involves investigators formulating a series of alternative propositions to questions concerning evidence in the course of a specific investigation. Using CAI, propositions are considered in pairs, one pertaining to a prosecution position, and another relating to a defence argument. Assessing the two propositions is intended to involve the generation of probabilities for each proposition pair given the evidence, as described in Section 3, which can then be expressed via Bayes Theorem together with likelihood ratios, which could inform investigator’s beliefs over whether they favour a prosecution or defence argument.

CAI was originally developed to meet two aims: first, to enable scientists and investigators to make more robust, testable and transparent judgments in pursuing police casework; and second, to enable police clients to pre­assess whether a particular scientific analysis might usefully inform an investigation³⁰. CAI frames evidence interpretation as a collaborative course of action involving consultation and input from forensic practitioners from the outset. This approach was contrasted with an older, police­led model of investigation, in which suspects were identified through markedly non­scientific means, with the collection and deployment of forensic evidence largely being directed to incriminate suspects³¹. These latter practices were viewed as unjust and unscientific.

During fieldwork in 2006-2010, the use of CAI was regarded by interviewees as beginning right from the outset of an investigation:

‘Say we just find a body in a field, what’s gone on? How did the body get there? What happened to the body? So they say well looking at the disturbance at the scene, I think the body’s been dragged from that position to that position, I then think it’s been turned over, you know, and all stuff like that³².’

Forensic Bayesian methods are intended to involve the consideration of prior probabilities ideally through relevant statistical data. As the interviewees comments above however demonstrate, making reconstructive inferences in casework often depended on one’s capacity to interpret a variety of visual cues in notably less quantitative ways. Another interviewee used the term, ‘soft data’ to describe this:

‘You can tell straight away that she’s probably been murdered, she’s clearly been sick, and somebody’s cleaned her up, she’s probably been re-dressed … that’s what that is, soft data, ‘why is the zip slightly down?’³³‘

Rather than prior probabilities in the form of statistics, the comprehension of soft data appeared to form an important preliminary step toward the formation of propositions. Soft data was found to depend strongly on how individual scientists visually apprehended a situation based on their experiential standpoint, which itself rested on a series of factors to which different individuals may be sensitised differently, including time, location, activity etc. Soft data was thus potentially unquantifiable and contingent. While fieldwork data used here is historical, more recent ethnographic research on homicide investigations strongly suggests that forensic investigators and police colleagues continue to rely on forms of soft data when initiating criminal casework³⁴.

CAI organises propositions into a hierarchy, classifying them as ‘source’ (relating to the origin of a piece of evidence), ‘activity’ (the manner in which that evidence was generated) and ‘offence’ (the extent to which evidence can indicate ultimate guilt or innocence) .

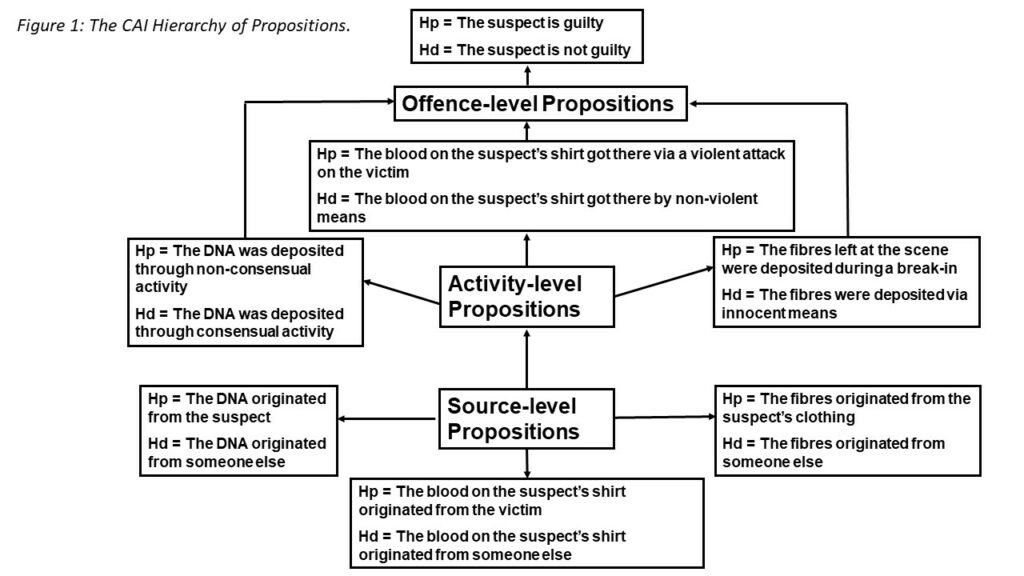
At each stage of the hierarchy, proposition pairs are intended to be evaluated using a Bayesian formula to generate an LR which may favour either the proposition or defence hypothesis. Figure 1 provides some examples of how these propositions may be expressed.

Source level (or ‘Level I’) propositions concern the origin of evidentiary material. A set of Level I propositions could concern the origin of a DNA profile found at a crime scene, with a prosecution hypothesis assuming that the probability the DNA originated from a suspect to be p=1, and a defence hypothesis involving the calculation of a random match probability to consider whether the DNA profile originated from someone else. Another example of a source level proposition relating to the shoeprint example would be a prosecution proposition ‘the shoeprint originated from the suspect’ with probability p=1, while a countering defence proposition could take the form ‘the shoeprint originated from someone else’ which could involve a probability estimate possibly involving consideration of the relative frequency of the particular shoe type and size in a certain population, similar to the example in Section 3. Consideration could also be given to the specific details of the shoeprint such as the level of wear on the suspect’s shoes.

The next level in the hierarchy of propositions, the activity level, or Level II, considers how the evidence came to be deposited at the scene. Activity level propositions relate to a more complex level of reconstructive reasoning. The transition from Level I to Level II may necessitate discussion between police investigators and forensic scientists in order to establish informative inferences. For example evaluating how DNA, whether it belonged to the suspect or another individual, came to be deposited at a crime scene, may open up various questions. If for example the DNA was found in connection with a suspected burglary, investigators may need to consider precisely where the DNA was found at the scene. If the DNA was found close to where damage to a property had occurred, and had been recovered from blood found near a broken window, a prosecution proposition may express the probability that the DNA was deposited in the act of breaking and entering. A defence proposition, on the other hand, may consider the probability that the individual under suspicion may have accidentally shed blood in the course of legitimately being nearby the premises.

The final level in the hierarchy, Level III or the offence level, concerns the probability that a suspect has committed a criminal offence. Level III propositions are the domain of the jury, assisted by the judge³⁵. Offence-level propositions may be expressed as activity-type propositions; however the key difference for Level III propositions is that they concern the question of whether an actual crime has occurred. In the CAI model offence-level propositions are regarded as beyond the realm of the forensic investigator and hence they represent a largely theoretical part of the framework. Investigators generally concern themselves with source (Level I) and activity (Level II) propositions. Level III nonetheless serves to help reinforce the rationale of the CAI process.

Applying this hierarchy however presented a series of challenges concerning the construction of propositions. A number of these issues related to how proposition construction exposed various forms of ambiguity. First, intra-propositional ambiguity concerned sources of semantic uncertainty within the wording of single propositions. For example, the word ‘contact’ was used as a problematic example. To propose that an individual ‘had been in contact with broken glass’ does not in itself convey clearly what the individual had exactly done to be in such contact, i.e. if they had deliberately broken a window or had been in the way as a bystander. Intra-propositional ambiguity may arise due to a lack of information at the activity level. If it is difficult to establish the precise series of events, scientists may only have recourse to more vague terms.

Second, inter-propositional ambiguity related to the challenges of formulating suitably corresponding pairs of prosecution and defence propositions. Issues were often encountered in formulating a defence proposition to account for an innocent explanation of how evidence came to be generated. Prosecution propositions often merely needed to express a probability of evidence being generated in the course of a criminal activity, whereas defence propositions could conceivably reflect a wide range of innocent explanations. To use an example from Figure 1, formulating a defence proposition to account for the presence of a victim’s blood on a suspect’s shirt could be faced with multiple possibilities, particularly if little is known about the case circumstances. The defence proposition could variously be that blood was deposited through the suspect trying to help the victim after an attack by someone else, or the seeming victim might have actually been an assaulter themselves, or that blood was deposited at an earlier date and the suspect may subsequently have borrowed the shirt. Proposition formation may also depend on variable factors which may be more or less well known, i.e. how well the two people knew each other, when they may have encountered each other, levels of intoxication etc. If knowledge of case circumstances is sketchy, it may be uncertain as to what activity-level defence proposition may be the most suitable.

Finally, statistical ambiguity related to the difficulties in determining which data to evaluate propositions. Data availability compounded this issue. One example discussed during fieldwork concerned a case involving the death of an elderly woman in the Netherlands. The woman was found dead in her greenhouse with two single stab wounds to the neck, seemingly administered by a pair of scissors. The woman had a history of substance abuse and had a high concentration of alcohol and diazepam in her system. Her husband, who also had a history of alcoholism as well as minor domestic violence, was placed under suspicion of her murder.

Three senior forensic scientists, together with a psychiatrist, a pathologist and a lawyer all deliberated over this case using CAI. Considerable difficulty was experienced in agreeing on which alternative propositions to formulate with regard to the case. However, the team agreed that a possible alternative to consider was that the woman had died accidentally.

A respondent, who had been a member of the investigative team, discussed the difficulty in acquiring statistics to compare the probabilities of murder versus an accident, in this case thought possibly to be a fall in which the scissors had accidentally stabbed the victim, who may have been holding the scissors, in the neck³⁶. One issue was that the investigators had only murder statistics for the UK and not for the Netherlands, the latter having a lower population and differing crime rates. Statistics on accident rates raised further issues. The investigators sought statistics on the number of accidents involving falls by women over the age of fifty. They could not however agree on whether those statistics were clear enough, as team members raised the question of whether those statistics would only include those admitted to hospital, and not all falls. The team also differed on whether or not the statistics accounted for the state of intoxication of individuals. The respondent recalled how the team found themselves having to construct propositions after it was determined which data were available, as opposed to agreeing on what propositions to test from the outset in accordance with formal Bayesian method. The respondent talked of ‘going backwards and forwards’ and thus the calculations were marked by a notable degree of contingency³⁷.

Eventually, the team settled on data which actually indicated the death was more likely to have been accidental. The respondent described how, in order to convince themselves of this explanation, they acted out falling and accidentally stabbing themselves with scissors. This respondent explicitly referred to how they had satisfied themselves that they had ‘Bayesianised’ the analysis despite this being based on an embodied, non-statistical form of reasoning.

CAI was intended as a means of managing beliefs through careful use of prior data, but fieldwork found that in practice reasoning was based on highly subjective and non-calculative epistemological foundations. In the course of applying CAI, investigators also became exposed to potentially intractable ambiguities and lacunae as they constructed propositions. Rather than testing the propositions they thought most ideal, investigators had to take a pragmatic approach, by testing those propositions that were seen to lie most within their means in terms of available data.

Recent research shows that the contingent and singular nature of criminal investigations continues to endure³⁸, and thus these lacunae continue to challenge the use of CAI. CAI has since nonetheless significantly informed practice guidelines set by international forensic scientific organisations³⁹. Bayes Theorem has also been used to develop automated forms of data processing such as for the interpretation of DNA profiles, as described next.

4.2. Forensic DNA Interpretation Technologies

Bayes Theorem has formed the algorithmic basis of technologies used to interpret complex forensic DNA profiles. Contemporary DNA analysis involves visualising DNA profiles in the form of a series of peaks using image analysis software in data traces known as electropherograms. Crime scene and individual suspect profiles can be compared by determining if peaks may line up vertically, which if all or most peaks do so, may suggest a match.

In practice certain issues can however complicate such analysis. DNA is highly susceptible to environmental degradation and contamination, and thus it may only be possible to discern a partial match between the crime scene DNA and a suspect profile. The amount of DNA that may be recovered from a crime scene is also highly variable, and may depend on where and how the DNA was deposited. Another factor is the biological source of the DNA. Bloodstains and saliva are potentially rich sources of DNA. The deposition of DNA through skin sweat may shed much lower quantities, although it may be possible to recover minute amounts through, for example, the act of someone touching a surface. So-called ‘Low Copy Number’ or ‘Low Template Number’ methods of recovering particularly minute quantities of DNA were developed by forensic laboratories, including the UK Forensic Science Service, from the late 1990s onwards to try and maximise the use of DNA in criminal investigations⁴⁰. Environmental degradation and contamination make low-quantity DNA analysis particularly challenging, but Bayes Theorem was applied to try and model DNA analysis at low quantities, using the kind of frameworks described in Section 3.

Another issue concerns the presence of mixtures of DNA from two or more individuals. This is frequently encountered in casework. A singular DNA profile represents an individual’s specific genotype. Determining genotypes, namely resolving which parts of a mixed DNA profile belong to which individual may be challenging, particularly where small quantities of DNA are involved. Automated expert systems have been developed to resolve genotypes in mixed DNA profiles. This can involve comparing the relative height of peaks in mixed DNA readouts. A consistently high series of peaks may correlate with one individual profile, while consistently lower peaks may correlate with another⁴¹. Bayesian statistical methods have been developed to model mixed DNA profiles, and these have formed the algorithmic basis of automated systems which are widely used in some jurisdictions, such as those of the USA⁴².

Analysis of scientific literature together with fieldwork highlighted issues with the systems and methods used to interpret complex low-quantity and/or mixed DNA profiles. These systems were developed to provide supposedly more robust methods of interpreting complex DNA profiles than through visual human interpretation. A first issue however concerns how individual DNA profile components (alleles) are identified on the electropherograms as peaks. Very small peaks may be disregarded as non-DNA anomalies or artefacts, as opposed to low volumes of actual DNA. Distinguishing non-DNA artefacts from actual DNA is however largely defined by the peak height threshold. Peaks may only be regarded as DNA if they are of a sufficient vertical height on the electropherogram. The peak height threshold can however be significantly localised, with individual laboratories setting different thresholds⁴³. The use of different peak height thresholds may lead to variation in whether analysts discern an artefact or genuine DNA component.

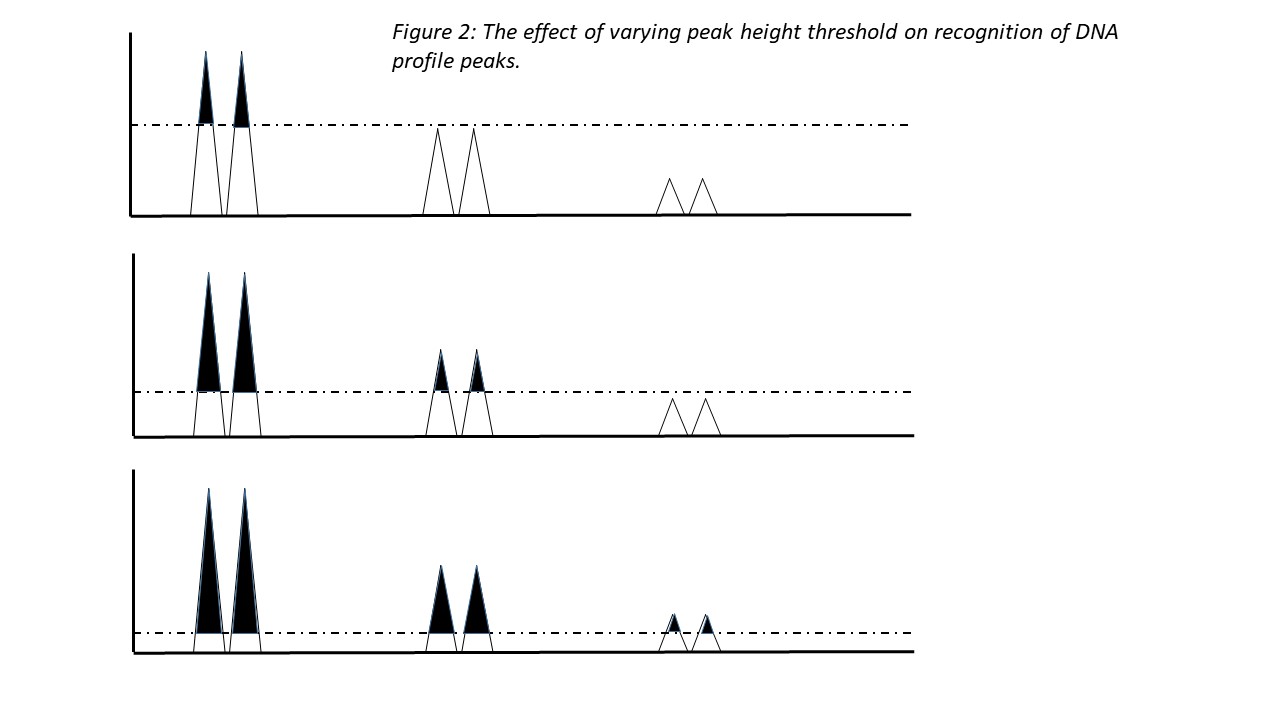
Thus even before Bayesian methods are applied, the perception of what constitutes DNA may vary between laboratories.

Second, analysing low quantities of forensic DNA profiles is hampered by the tendency for individual alleles not to be detected, leading only to a partial profile, but also for contaminating DNA elements to feature disproportionately within the profile. When modelling low-template DNA analysis, some scientists incorporated the probability that alleles could either ‘drop out’ (Pr(D)) or ‘drop in’ (Pr(C)) to a low-template DNA profile, into their Bayesian models⁴⁴. What did not however appear to be considered is the possibility that certain alleles may be more probable to drop-out than others. Each individual allele consists of a specific pattern based on the building blocks of DNA (of which there are four, designated ‘A’, ‘C’, ‘G’ and ‘T’). These patterns may vary considerably in complexity and size. The system developed by the FSS did not appear to take into account the possibility that some alleles could be more probable to drop-out than others. The models did not seem to account for smaller alleles being more liable to drop-out than larger ones, or that larger alleles might degrade, losing part of their pattern so that they might resemble smaller alleles in the data trace.

This FSS system moreover modelled the probability for a specific allele to drop in based on their frequency in the white Caucasian population. This however raises issues which are still ongoing. Much scientific debate has involved the relative frequency in which certain alleles occur in different ethnic groups. Categorising allele frequencies by ethnicity is however beset by the issue that ethnic categories are based on decidedly sociocultural classifications, which has been argued to be tautologous, raising further questions about the validity of such models⁴⁵.

Analysing DNA mixtures in forensic work using Bayesian algorithms involves estimating the probability that certain parts of a mixed DNA profile belong to one contributor, and the probability that other elements belong to others. This is complicated by having to consider such probabilities in relation to both prosecution and defence hypotheses⁴⁶. This entails determining the ratio of the relative contributions of two or more individuals. If for example a mixture is thought to contain DNA of a possible suspect and victim, it may be that one or the other may contribute significantly more to the mixture. This may be ascertained via comparison of relative peak heights. This may not however always be straightforward if all peak heights are similar, and analysis could be significantly complicated further if the mixture is thought to contain three or more contributors. Judging mixture proportion or ratio may also be complicated by the differing size of alleles at different loci. One contributor may exhibit a large-size allele at one locus, while another contributor might exhibit a large-size allele at another locus. At each point in a DNA profile (or locus), an individual possesses a pair of alleles. These alleles can be different at each locus (heterozygous), or the individual may possess an identical pair (homozygous). On an electropherogram, this appears as a pair of peaks for heterozygous pairs or as one large peak if homozygous. These different data representations may also greatly complicate the use of a Bayesian analysis.

The challenges to interpreting low-template and mixed DNA profiles, as reported in older fieldwork and scientific literature were found to endure in more recent research carried out by the author and others⁴⁷, despite evidence from automated systems now being frequently presented in court cases⁴⁸. As DNA detection methods have become more sensitive, detecting low-quantity and mixed DNA profiles has become more common, leading to interpretation issues including drop-in and drop-out being experienced more frequently⁴⁹. Contemporary probabilistic systems claim to be able to calculate the probabilities of an array of different individual genotypes existing within mixtures, which may entail considering large numbers of permutations of peaks beyond the capability of human analysts. The functioning of Bayesian algorithms however remains highly situated. Laboratories continue to vary in terms of how they set key analytical parameters, notably peak height threshold⁵⁰. A recent (2023) comparison by Thompson of two of the most widely used probabilistic systems, STRMix™ and TrueAllele™, found considerably wide variance in generated likelihood ratios when mixed DNA casework samples were analysed, both between the two systems and within repeated uses of TrueAllele™ alone. Thompson suggested that variable parameters and assumptions on the part of laboratories and analysts, including peak height threshold, but also prior assumed number of contributors, mixture ratio and drop-in probability, could all play a role in this variance⁵¹. It should also be noted that while there has been vastly increasing interest in characterising the DNA of whole populations on the basis of ethnicity, recent fieldwork suggested that the arguably tautologous relationship between genetic and sociocultural categorisation seemingly remains unquestioned by scientists⁵².

Thus while technology has advanced, Bayesian DNA interpretation algorithms continue to rely on a series of contestable ontological assumptions and variable localised practices. These systems are nonetheless now frequently used to provide evidence in cases involving serious alleged crimes where significant matters of liberty and possibly life are at stake, particularly in western jurisdictions. These Bayesian technologies hence serve to reinforce social orders of both scientific and legal hegemony.

The next section reflects on the wider implications of the two examples discussed in this article.

 

5. Discussion

This article has sought to critically explore the enactment of Bayes Theorem in forensic science, which has been valorised for its supposedly inevitable logicality and capacity to manage beliefs about criminal cases. Forensic Bayesianism is based on the principle that any prosecution proposition should be compared against a corresponding defence proposition. The two examples presented here however show that the bare algebraic forms of forensic Bayesianism struggle to account for significant epistemological and ontological complexity.

In these instances, forensic Bayesianism complicated rather than systematised the evaluation of belief by exposing the inability to gain complete access to necessary data. In its place investigators and analysts had to draw upon subjective experience, or fragmented and incomplete data, or allowed localised and problematic assumptions to be perpetuated within Bayesian frameworks.

Applying Bayes Theorem to forensic casework through CAI involved sometimes incalculable epistemological underpinnings and exposed reasoners to potentially intractable lacunae. In one case, embodied enactment was required to recognise a seemingly counterintuitive Bayesian outcome. Here Bayes Theorem destabilised hitherto taken for granted representative practices by disrupting an assumed stable and manageable relationship between subjective reason and data. These findings contrast with those of Kruse ⁵³ (see Section 1). Rather than functioning as an ordering mechanism, here forensic Bayesianism exposed contingencies rather than facilitating epistemic routine. Following Latour⁵⁴, the ambiguities and uncertainties which CAI exposed were akin to opening up numerous previously stable or ‘black boxed’ forms of evidential analysis.

In the second example, the incorporation of Bayes Theorem into forensic DNA interpretation algorithms mediated representative practices which obscured questionable analytical assumptions. Bayes Theorem contributed to the construction of technical black boxes by hiding these assumptions within the ostensibly immutable form of electropherograms and likelihood ratio statistics. Recent research, such as that of Thompson (2023) and the author, has found however that the black-boxed status of these systems remain susceptible to being challenged.

Bayes Theorem was applied to forensic science as it was regarded by proponents as ideally suited to give an epistemologically robust voice to evidence. This article however suggests that it actually disrupts and destabilises the black box status of forensic science. This is ironically a consequence of the western judicial state’s struggle to construct and control material witnessing. Western judicial power has become ever more dependent on the claimed epistemic authority of science and technology⁵⁵. The imaginary of scientific evidence, such as DNA, to be inert ‘silent witnesses’ which nonetheless present immutable ‘truths’ is a well-worn trope which comfortably aligns with the ideal of a hybrid technolegal form of authority⁵⁶. The expressed notion that Bayes Theorem is the ‘only logical way’ to reason about evidence also emphasises a projected inevitability of scientific determinism in judicial decision-making⁵⁷. The problem however is that forensic Bayesianism may not function as an unproblematic, straightforward or strictly linear logic. This is largely due to Bayes Theorem imposing heavy and intractable informational demands when applied to the analysis of material evidence. Generating the kind of probabilities in forensic contexts, as idealised in scientific literature, actually requires extensive background data, for example on the frequency of particular DNA components in a certain population, the frequency of a particular shoe type in a local area, or data on how a certain type of glass fragments. Some data may be even more elusive, such as the differential susceptibility to environmental degradation among differently sized DNA components, or on what constitutes a genuine DNA component on an electropherogram rather than an artefact or contaminant. Sometimes prior data may be incalculable, as in the examples of soft data.
In the absence of perfect data, we have seen how investigators may resort to contingent or improvised practices, or allow contestable assumptions to hold. Rather than facilitating linear and systematic computation, forensic Bayesianism poses further questions of investigators and even of technology itself, as in the example of the differing results produced by different DNA algorithms⁵⁸. When dealing with material evidence, law enforcement finds itself having to give a voice to supposedly self-explanatory silent witnesses. But here the ways in which the judicial state tried to do so either undermined or problematised the imagined epistemic and moral authority of scientific justice.

6. Conclusion

The instances of forensic Bayesianism discussed in this article bestowed equivocal voices to material evidence. In the example of CAI, investigators found themselves in circular conversations with evidence, where the evidence asked questions of them in terms of what it actually was. The incorporation of Bayes Theorem into DNA interpretation algorithms gave evidence a potentially skewed and discriminatory voice. Rather than providing a systematic form of mediating subjective belief with data, this article instead found that forensic Bayesianism created messy entanglements between evidence, place and subjectivity. It destabilised practices of material witnessing by disruptively reconfiguring the relationship between seeing and testifying. Giving a voice to evidence through Bayes Theorem depended on the ways and experiences of seeing and visualising on the part of analysts. Yet in return Bayes Theorem shaped seeing in highly unpredictable ways, such as stimulating embodied enactment, or by masking ontological questions that lay within DNA data readouts. These conclusions not only reflect how the western judicial state continues to grapple with maintaining epistemic authority, but they also have significance for counter-hegemonic forms of forensic practice⁵⁹. These findings re-affirm the primacy of the visual, the aesthetic, the situated and the embodied in engaging with materiality as a form of witnessing. But this article adds an important note of caution for how alternative forensic practices should engage with the calculative, and warns against regarding Bayesian computation as an unproblematically accountable means of managing material witnessing.

 

Biography
Christopher Lawless is an Associate Professor within the Department of Sociology, Durham University. He originally trained as an analytical biochemist before gaining a PhD in Sociology. He has researched the sociology of forensic science and biometric technology for almost nineteen years, and draws upon conceptual resources from Science and Technology Studies. He has also conducted research related to critical infrastructures and climate change.

Notes